79
CHAPTER 3:
CATEGORICAL INFERENCES
Inference is the process by which the truth of one proposition (the conclusion) is affirmed
on the basis of the truth of one or more other propositions that serve as its premise or
premises. When a conclusion is drawn from only one premise, the inference is said to be
immediate. Where there is more than one premise involved, the inference is said to be
mediate. This chapter will study these two forms of argument in categorical logic.
A. Arguments Expressing Immediate Inference
We will consider three kinds of immediate inferences:
1. Immediate inferences embodied in the square of opposition
2. Obversion
3. Conversion
I. Introduction to the Traditional Square of Opposition.
In everyday life, we come across many complex issues. People express their opinions
about them in statements or propositions. Let us take the issue of war, for example. Some
are opposed to all forms of violence. And they express their position on war by defending
the proposition that “All wars are unjust.” This is a pacifist position. On the other hand,
others might associate themselves more closely with Social Darwinism, believing that
evolution is through survival of the fittest and that “No war is unjust.” However, someone
who attempted to defend both propositions would be inconsistent: “All wars are unjust
and “no wars are unjust” cannot both be true.
Now suppose Alicia asserts that “Some wars are unjust.” Should we take this to imply
that she believes “Some wars are not unjust”? Does the truth of “Some men are fathers”

80
imply that “Some men are not fathers” is also true? It is a common fallacy to assume that
the truth of a statement of the form “Some S are P” necessarily implies the truth of the
statement with form “Some S are not P.” Thus, many find it difficult to accept the truth of
“Some fathers are men” because they misleadingly believe this would imply that they
accept “Some fathers are not men” as true.
Debates in morality, science, politics, and other areas underscore the importance of
knowing what can be validly inferred from the assertion of a given proposition. Civil
debates are the way we exchange ideas and persuade others. They emphasize the
importance of knowing how to present, defend, and reject contentious claims. The
traditional square of opposition is an important tool in understanding the logical
relationships between categorical propositions with the same subject and predicate.
II. The Four Kinds of Opposition
There are four kinds of categorical propositions, first introduced in Chapter Two: A, E, I,
and O.
A: All S are P Universal Affirmative
E: No S are P (All S are not P) Universal Negative
I: Some S are P Particular Affirmative
O: Some S are not P Particular Negative
Each of these propositions can serve as a premise for immediate inference. Thus, if an A
proposition is used as a premise, then one can immediately infer that the corresponding O
proposition (having the same subject and predicate terms as the A) is false. To illustrate,
if the A proposition: “All car salesmen are liars” is given as true, then the O proposition:
“Some car salesmen are not liars” must be false.
The traditional square of opposition provides a basis for this kind of immediate inference.
The term “opposition” was used by classical logicians to apply to the differences in
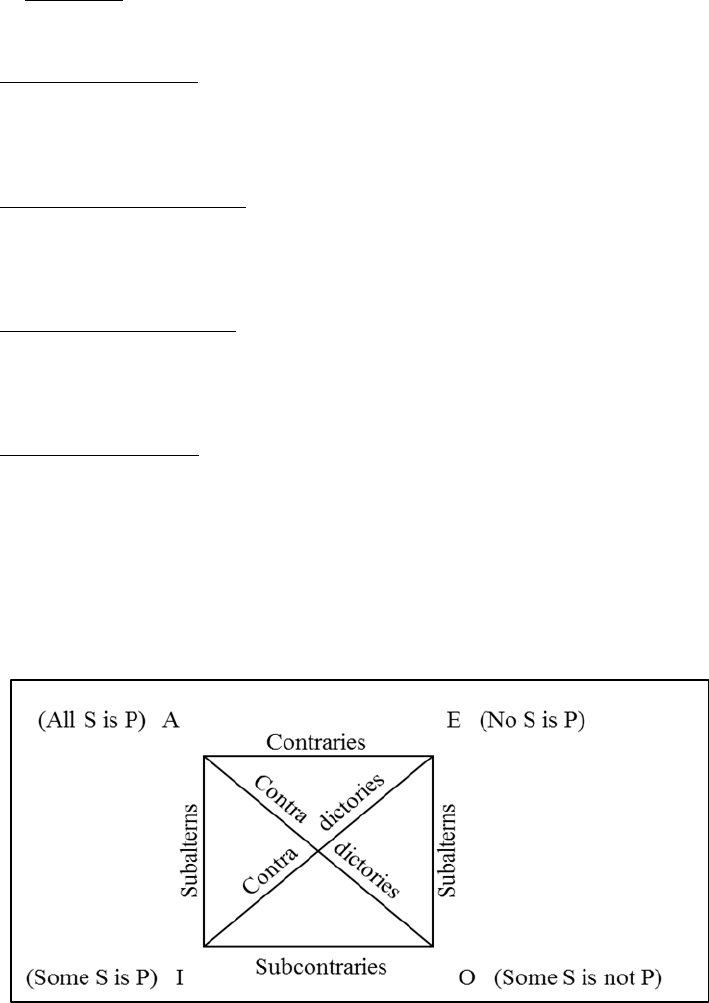
81
quality (affirmative or negative) and quantity (universal or particular) between standard-
form categorical propositions having the same subject and predicate terms.
There are four kinds of opposition:
1. Contrary Opposition is opposition between two universals of different quality (A
and E).
2. Contradictory Opposition is that between a universal and a particular of different
quality (A and O; E and I).
3. Subcontrary Opposition is opposition between two particulars of different quality
(I and O).
4. Subaltern opposition is that between a universal and a particular of the same
quality (A and I; E and O).
These various kinds of opposition can best be illustrated by a diagram called the Square
of Opposition as shown below:
Figure 3.1
82
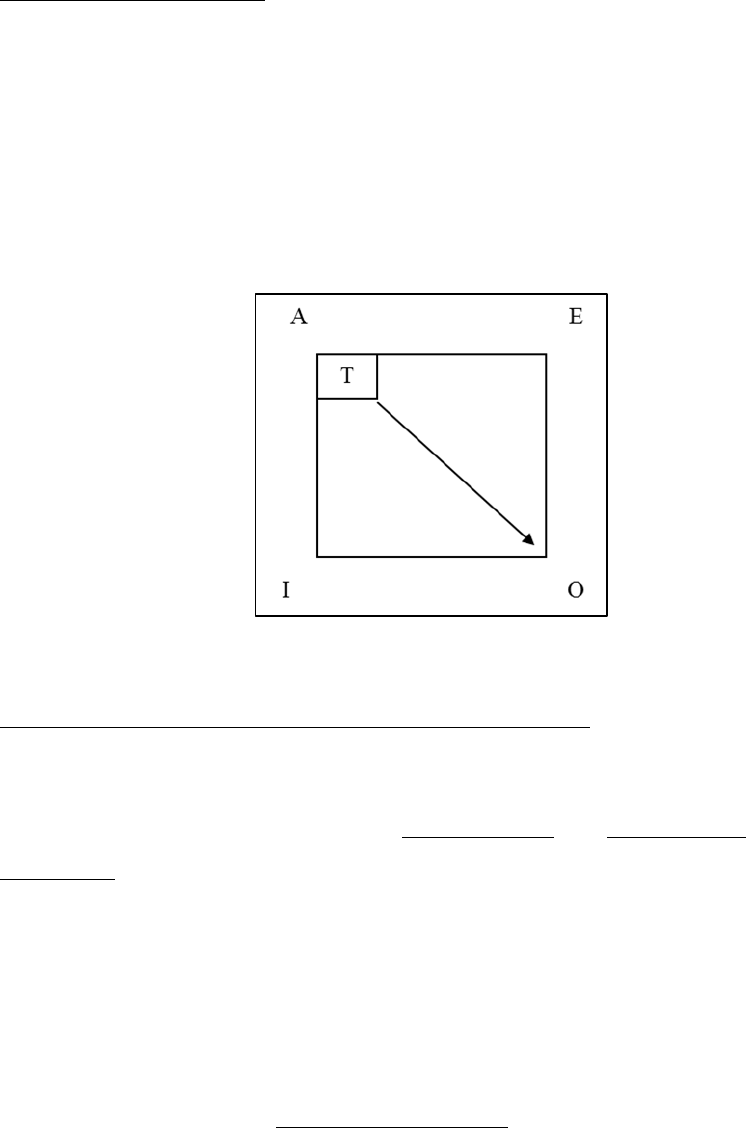
III. Rules of Opposition
We can derive rules of immediate inference for each of the four types of opposition
mentioned above. These inferences will be from a premise to a conclusion. The premise
will be indicated by enclosing its truth-value in a small box within the square as shown:
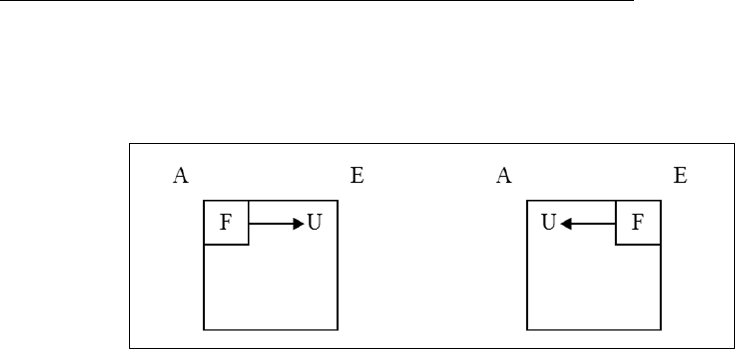
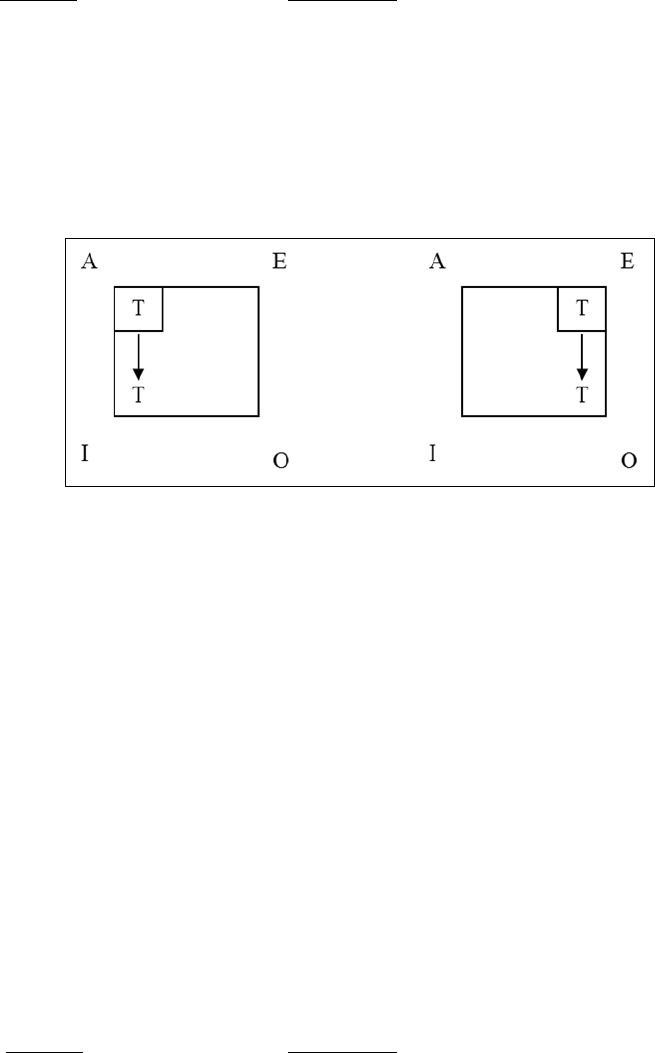
Example: In the diagram, the A proposition is the premise. We read it as: “Given the A
as true, therefore, the O is. . .”
Figure 3.2
Deriving the Rules of Inference for Contradictory Opposition
Contradictory Opposition is that between the A and the O, and the E and the I
proposition. Let us consider the A and the O first.
If the statement, “All coins in my pocket are quarters” (A proposition), is true, what can
be inferred about the opposed statement, "Some coins in my pocket are not quarters" (O
proposition)? True or False? It requires little reflection to see that if the A is true, then the
O cannot also be true. And it is equally as easy to see that if the O is true (Some coins in
my pocket are not quarters), then the A must be false (All coins in my pocket are
quarters).
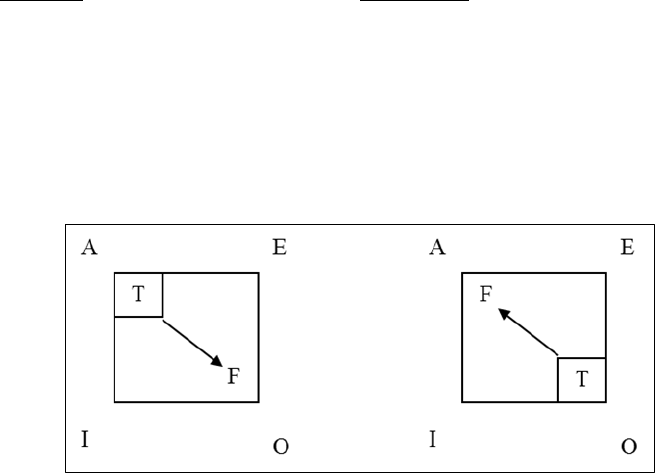
83
We can summarize our analysis in a table as follows:
Premise Conclusion
Given A as true, therefore O is false.
Given O as true, therefore A is false.
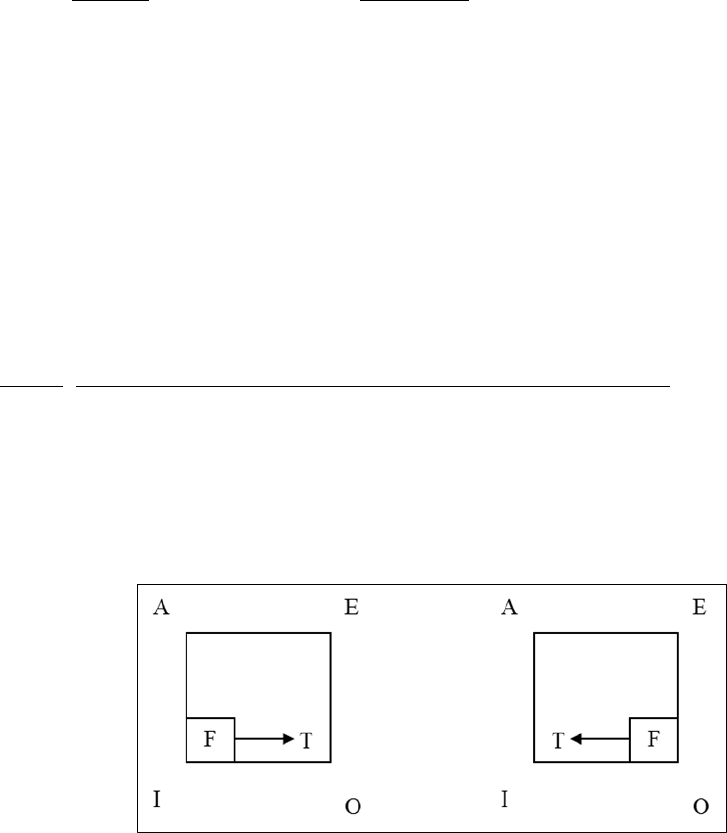
Using the square, we can illustrate the inference thus:
Figure 3.3
The truth-value in the small box shows the truth-value of the premise, and the truth-value
outside the box is the truth-value of the possible conclusions. The arrow shows the
direction of the inference.
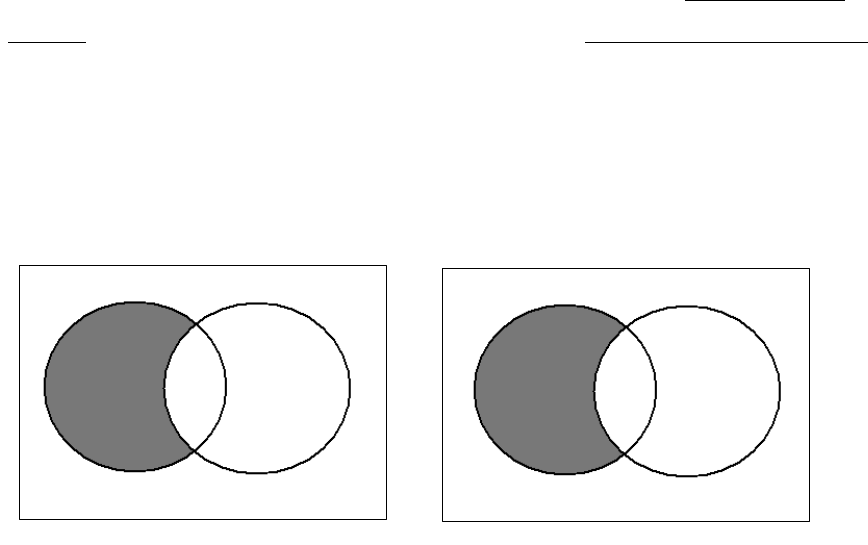
Let us next consider the E and I Contradictories:
E: No coins in my pocket are quarters.
I: Some coins in my pocket are quarters.
Again, it is easy to see that if the E is given as true, the I cannot also be true, and if the I
is given as true, the E cannot also be true.
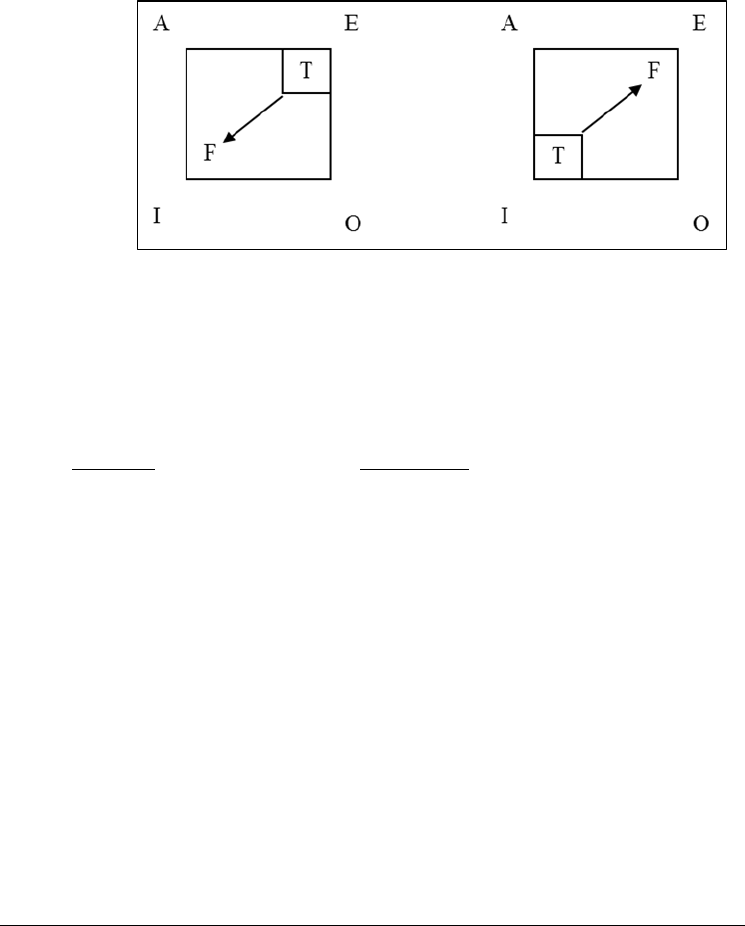
84
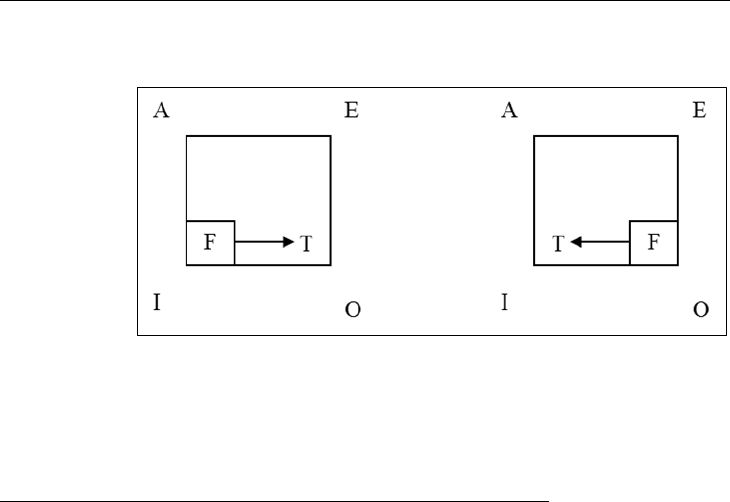
Using the Square, we can illustrate this in the following manner:
Figure 3.4
Combining the A and O and E and I inferences into a table we have:
Premise Conclusion
Given A as true, therefore O is false
Given E as true, therefore I is false
Given I as true, therefore E is false
Given O as true, therefore A is false
Observe from the table that the premise and the conclusion cannot both be true at the
same time. From this observation, we can now formulate the first rule for contradictory
opposition as follows:
Rule 1: CONTRADICTORY PROPOSITIONS CANNOT BOTH BE TRUE.
So far, we have been considering the premises to be true. Suppose now that the premises
were given as false, then what conclusion can we infer? If A is false, what is O? If O is
false, what is A? If E is false, what is I? And if I is false, what is E? Again, let us consider
our example above to see what inference we can make.
85
If the A proposition “All coins in my pocket are quarters” is false, then, what can we
infer about the corresponding O proposition “Some coins in my pocket are not quarters”?
Clearly, we can infer that the O must be true. And if the O is given as false, it is easy to
see that the A must necessarily be true.
Let us next consider the E Proposition “No coins in my pocket are quarters” to be false.
Then, what can we infer about the I Proposition “Some coins in my pocket are quarters”?
Clearly, if the E is false, then the I must be true.
We can sum up the result of the above analysis in the following table:
Premises Conclusion
Given A as false, therefore O is true.
Given E as false, therefore I is true.
Given I as false, therefore E is true.
Given O as false, therefore A is true.
Observe from the table that the premise and the conclusion cannot both be false at the
same time. From this we can now formulate the second rule for contradictory opposition
as follows.
Rule 2: CONTRADICTORY PROPOSITIONS CANNOT BOTH BE FALSE.
The rule can be summarized in terms of the Square as follows:
Figure 3.5
A E A E A E A E
I 0 I 0 I 0 I 0
T
F
F
T
F
T
F
T

86
Deriving the Rules of Inference for Contrary Opposition
Contrary Opposition is the opposition between the A and the E. Now, if A is given as
true, what is E? And if the E is given as true, what is A?
Again, let us use the concrete example given above. Thus, if the A (All coins in my
pocket are quarters) is true, then what can be inferred about E (No coins in my pocket are
quarters)? Well, if it is true that “All coins in my pocket are quarters,” then it is
necessarily false that none are quarters. Similarly, if it is true that “No coins in my pocket
are quarters,” then it is necessarily false to say that “All coins in my pocket are quarters.”
We can summarize the inferences in following table:
Premise Conclusion
Given A as true, therefore E is false.
Given E as true, therefore A is false.
Observe in the table that the premise and the conclusion cannot both be true at the same
time. We can thus formulate our first rule as follows:
Rule 1: CONTRARY PROPOSITIONS CANNOT BOTH BE TRUE.
Using the Square to illustrate the rule, we have:
Figure 3.6
87
Let us now consider the premises to be given as false. Thus, if A is given as false, what
can we infer about E? And if E is false, what can we infer about A? To help us in our
analysis, let us again use the example above.
Consider the A statement “All coins in my pocket are quarters” to be false.
Does it follow that none of the coins in my pocket are quarters (E)? No, we cannot
necessarily infer this to be true, because it could also be the case that only some coins are
quarters (I) while the rest are not (O).
Thus, the statement, “All coins in my pocket are quarters” is false if either (1) “No coins
in my pocket are quarters” (E) is true, or 2) “Some coins in my pocket are not quarters
(O) is true. If we know that an A proposition is false we can conclude that the
corresponding O proposition must be true. But we cannot conclude that the
corresponding E proposition must be true. All we can conclude is that it is possible for E
to be true, but it is also possible for E to be false. Indeed, A and E could both be false.
Our analysis above also holds also if E is false. We cannot use this to infer that A must be
true. All we can conclude is that it is possible for A to be true, but it is also possible for it
to be false. Thus, E and A could both be false. To see this, consider that the E statement,
“No coins in my pocket are quarters” is false if 1) All coins in my pocket are quarters is
true (A), or 2) Some coins in my pocket are not quarters is true (O). Since we cannot
determine by logic alone which condition is the case, the truth of A is undetermined by
the falsity of E.
We can summarize our analysis in a table as follows:
Premise Conclusion
Given A as false, therefore E is undetermined (could be false or true).
Given E as false, therefore A is undetermined (could be false or true).
88
Rule 2: CONTRARY PROPOSITIONS CAN BOTH BE FALSE.
Using the Square to illustrate the rule we have:
Figure 3.7
Deriving the Rules of Inference for Subcontrary Opposition
Subcontrary Opposition is opposition between the I and the O propositions. Let us see
what we can infer if the premises are taken as true. Consider the following example:
Suppose we assume that the I proposition “Some planets are things that have moisture”
(I) is true. What can we infer about the truth or falsity of the O proposition "Some planets
are not things that have moisture"? Can we infer the O to be true? No, because further
exploration might prove that all planets have moisture (A). If this is the case, then the O
proposition would not be true.
Can we infer then that the O proposition is false? We cannot infer this either since further
exploration might prove that, in fact, some planets are actually dry, in which case the O
proposition would be true.
If the I proposition is given as true, the O proposition could be false or could be true. We
cannot determine which is the case by logical inference alone.
89
It is similar in cases where the O is assumed true. Thus, if the statement, “Some planets
are not dry places” is true (O), we cannot infer that the statement "Some planets are dry
places" is true (I). For future investigation, might prove that “No planets are dry places"
(E) is true, in which case, the I proposition would necessarily be false. Thus, if the O is
given as true, the truth-value of the corresponding I proposition is undetermined. That is,
it could be true or it could be false.
Summarizing the result of our analysis, we have:
Premise Conclusion
Given I as true, therefore O is undetermined.
Given O as true, therefore I is undetermined.
Observe that because the conclusion is undetermined, it is possible for both subcontraries
to be true at the same time. Thus, given the I as true, the O can be true, and given the O as
true, the I can be true. From this observation, we can formulate the first rule as follows:
Rule 3: SUBCONTRARY PROPOSITIONS CAN BOTH BE TRUE.
The square of opposition can be used to illustrate the rule as follows:
Figure 3.8

90
It might be worth repeating here that contrary to common belief, we cannot infer the truth
of one subcontrary from another. For example, from the truth of the statement, “Some
people are rich,” we cannot infer the truth of its subcontrary, namely, “Some people are
not rich." This latter statement is true, not as an inference from the truth of the
subcontrary I proposition but from an independent source of knowledge, namely, our
knowledge that there are, in fact, some people who are not rich. Likewise, given the truth
of the statement “Some marbles in my pocket are red” it does not necessarily follow that
“Some marbles in my pocket are not red.”
Now consider the case where the premises are assumed to be false. If the statement,
“Some coins in my pocket are quarters” is false, what can we infer about the statement,
“Some coins in my pocket are not quarters”? If it is false that some coins in my pocket
are quarters, then it follows necessarily that no coins in my pocket are quarters. If it is
true to say that no coins in my pocket are quarters, it is also necessarily true that some
coins in my pocket are not quarters. So, if I is given as false, then O is necessarily true.
What if an O proposition is assumed false? For example, suppose “Some coins in my
pocket are not quarters” is false. Then, it follows necessarily that all the coins in my
pocket are quarters. If it is true that all of the coins in my pocket are quarters, it follows
that some of the coins in my pocket are quarters must be true. Thus, if O is given as false,
then I is necessarily true. Summarizing the inferences in a table, we have:
Premise Conclusion
Given I as false, therefore O is true.
Given O as false, therefore I is true.
From this we can formulate the second rule as follows:
91
Rule 4: SUBCONTRARY PROPOSITIONS CANNOT BOTH BE FALSE.
Figure 3.9
Deriving the Rules of Inference for Subaltern Opposition
Subaltern Opposition is opposition between the A and the I and between the E and the O
propositions. If A is given as true, what can we infer about the corresponding I
proposition? And if E is assumed true, what can we infer about the truth of the
corresponding O?
Assuming the statement “All coins in my pocket are quarters” to be true, we can infer
that “Some coins in my pocket are quarters” must be true. Similarly, if “No coins in my
pocket are quarters” is true, then it must be true that “Some coins in my pocket are not
quarters.”
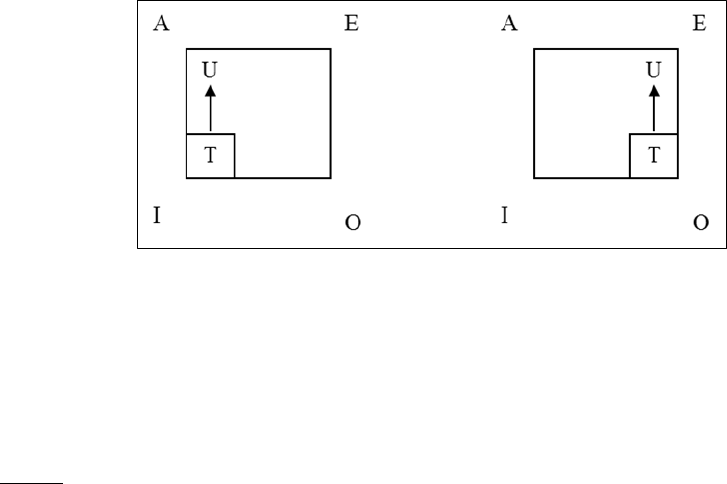
Next, take the I and the O as premises. Thus, if I is assumed true, what can we infer about
the truth or falsity of the corresponding A proposition? And if the O is assumed true,
what can we infer about the truth-value of the corresponding E proposition?
92
We can summarize our inferences in a table as follows:
Premise Conclusion
Given A as true, therefore I is true.
Given E as true, therefore O is true.
Using the square to illustrate the inferences, we have:
Figure 3.10
Assume now that the I and the O propositions are true. If the statement, “Some planets
are things that have moisture” is true, can we infer that the A statement, “All planets are
things that have moisture” is also true? Certainly not, since it remains possible that some
planets do not have moisture. But can we infer that the A proposition is false? We cannot
infer this either since it is also possible that further investigation may, in fact, prove that
all planets are moist places. Thus, if the I is true, then the truth-value of the A proposition
is undetermined.
Similarly, from the truth of the statement, “Some planets are not dry,” we cannot infer
that “No planets are dry” is true. The truth of the O proposition leaves the truth of the E
proposition undetermined. We can summarize our analysis in the following manner:
Premise Conclusion
Given I as true, therefore A is undetermined.
Given O as true, therefore E is undetermined.
93
Using the Square to illustrate these inferential relationships, we have:
Figure 3.11
Rule 1 summarizes the cases in which the premises are taken as true:
Rule 1: GIVEN THE UNIVERSAL AS TRUE, ITS PARTICULAR MUST BE
TRUE.
GIVEN THE PARTICULAR AS TRUE, ITS UNIVERSAL IS
UNDETERMINED.
Note: The first part of the rule makes the existential assumption. See part B of this
chapter where this is discussed.
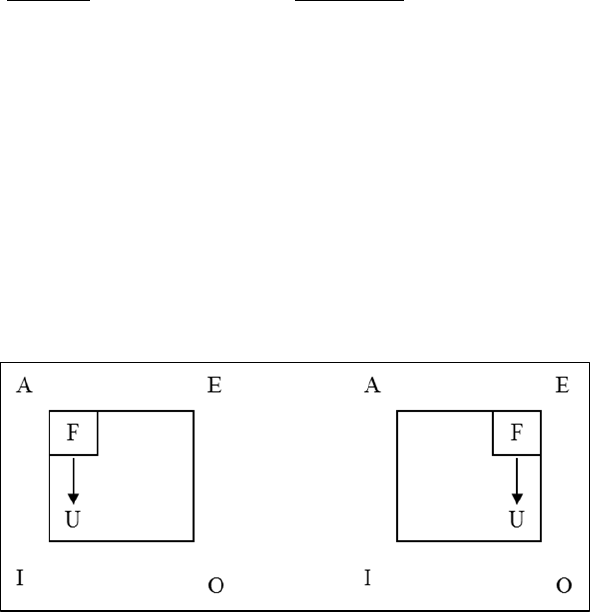
Let us now examine cases where the premises are assumed to be false. First, assume the
A statement, “All coins in my pocket are quarters” to be false. As we analyzed earlier
under contrary opposition, if the statement is false, then one of the two following
statements is true: 1) No coins in my pocket are quarters (E), or 2) Some coins in my
pocket are not quarters (I). Since we cannot logically infer which of the two conditions is
the case, all we can conclude is that if the A is false, then the truth or falsity of the E and I
is undetermined.
94
Our analysis also holds true if the E is given as false. Thus, if “No coins in my pocket are
quarters” is false, then, either “All coins in my pocket are quarters” (A) is true or “Some
coins in my pocket are quarters” (O) is true. Since we cannot infer whether the A is true
given that the E is false, we cannot infer the truth-value of the O. The truth value of O is
undetermined by the falsity of E: O could be true or O could be false.
Summarizing our analysis in a table we have:
Premise Conclusion
Given A as false, therefore I is undetermined.
Given E as false, therefore O is undetermined.
Using the Square to illustrate the inferences, we have:
Figure 3.12
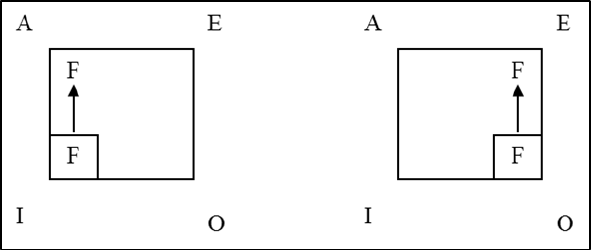
Secondly, let us assume that the premises I and O are false. If the I statement, “Some
coins in my pocket are quarters” is false, then what is the truth-value of the A statement
“All coins in my pocket are quarters”? It must be false. I cannot hold that “All coins in
my pocket are quarters” is true if we have assumed that “Some coins in my pocket are
quarters” is false. Likewise, if the O is assumed false, the E is necessarily false.
95
We can summarize our analysis in a table as follows:
Premise
Conclusion
Given I as false, therefore A is false.
Given O as false, therefore E is false
Using the Square to illustrate the table we have:
Figure 3.13
We can now formulate the second rule for subaltern opposition.
Rule 2: GIVEN THE UNIVERSAL AS FALSE, ITS PARTICULAR MUST BE
UNDETERMINED.
GIVEN THE PARTICULAR AS FALSE, ITS UNIVERSAL MUST BE
FALSE.
There are two methods of outlining inferences from the Square of Opposition, and a
summary of both appear on the next page. First, there is the table, which is read across
from the premise to the various conclusions that can be inferred from the one premise.
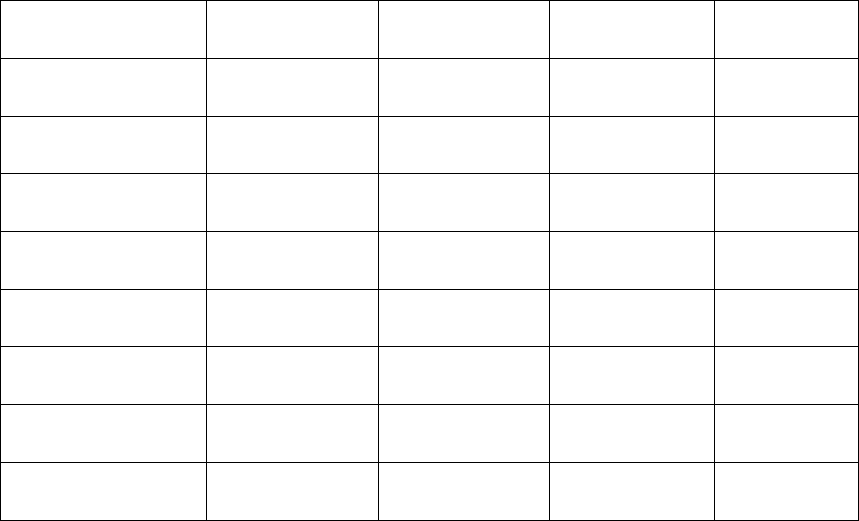
96
The second outline is by means of squares. Observe that the arrows point to the logical
inferences that can be made from a given premise. For example, from A as true, I can
infer E as false and I as true. Or, having inferred I as true, I can then use it as a premise to
infer E as false (rule of contradiction).
Square of Opposition Table
Premise Conclusions
A
E
I
O
A true, therefore
True
False
True
False
E true, therefore
False
True
False
True
I true, therefore
Undetermined
False
True
Undetermined
O true, therefore
False
Undetermined
Undetermined
True
A false, therefore
False
Undetermined
Undetermined
True
E false, therefore
Undetermined
False
True
Undetermined
I false, therefore
False
True
False
True
O false, therefore
True
False
True
False
Figure 3.14
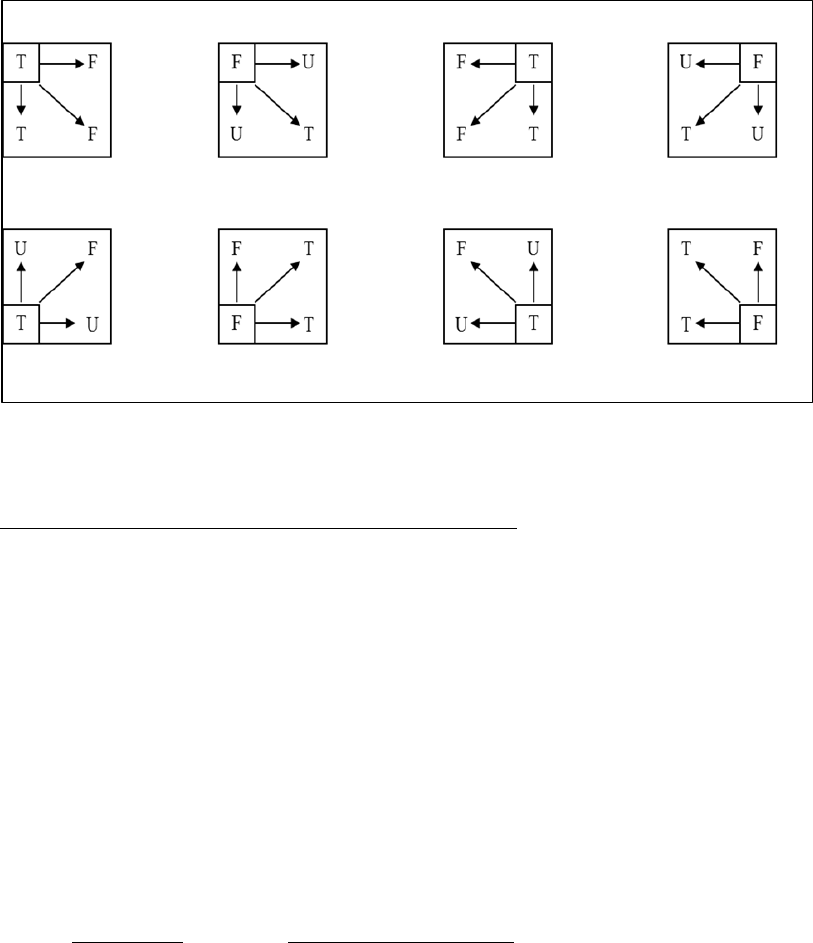
97
We can also summarize the rules graphically by using the square:
1 2 3 4
5 6 7 8
Figure 3.15
Practical Application of the Square of the Opposition.
One useful application of the table of opposition is the clear indication of how to refute a
proposition. In debates and discussions, propositions with regard to certain issues are
often assumed, for example, “All handguns should be banned,” “No abortions should be
funded,” “All wars are unjust,” “All forms of free-enterprise benefit the poor” and so on.
The rules of opposition show that the only propositions that cannot both be true are
contraries and contradictories. It follows that the only way to refute any proposition is to
establish the truth of either its contrary or its contradictory. Let us summarize this in the
following table:
Proposition Refuted by the Truth of Squares
A E or O 3, 7, 6
E A or I 1, 5, 8
I E 3
O A 1
98
1. Observe that the I proposition cannot be refuted by an O or the O by the I. The
reason is that both subcontrary propositions could be true. Thus, “Some horses are
colts,” and “Some horses are not colts,” are both true.
2. Observe that though the A proposition can be refuted by the E and the E by the
A, there is the possibility that we may be refuting one false proposition by
another. The reason is that both contrary propositions could be false. We cannot
infer that if A is false, E is necessarily true. Thus, in trying to refute an A by an E,
which is certainly possible, one must be sure of all of the facts. If you decide to
refute the Freudian claim that “All forms of religion are infantile” (A), by giving
its contrary, “No forms of religion are infantile,” you must be sure that every
instance of religion is not infantile– a very difficult, if not impossible claim to
establish. This leads us to the next observation.
3. An easier and more practical method of disproving an A or E is to establish its
contradictory. All you need do here is to give one instance which would contradict
the A or E.
At this point, one might ask if we cannot equally refute an A by showing its subalternant
I to be false. If it can be shown that I is false, it follows that the A proposition is false.
But this procedure is really the same as establishing the contrary to be true. In other
words, to prove that the I is false, you have to show that the E is true.
4. In an argument or debate, it is wise to avoid making universal statements (A or E)
unless you are reasonably sure of all instances. Otherwise all your opponent has to do
to refute you is to give one contradictory instance.
5. Hedge your statements by phrases such as, “For the most part,” “In general…”,
and “In most cases.. . .” . The resulting statements are either I or O propositions
and are difficult to refute because this would require proving that the A or E
universal propositions must be true.

99
3.A.1. Exercises: Square of Opposition:
Answer the following:
1. Illustrate each of the four types of opposition.
2. How does one refute an A proposition?
3. How does one refute an E proposition?
4. How does one refute an I proposition?
5. How does one refute an O proposition?

100
3.A.2. Exercises: Decide whether the following inferences are valid or invalid:
1. Given A as false, therefore E is true. _____
2. Given E as true, therefore O is false. _____
3. Given I as true, therefore O is true. _____
4. Given O as false, therefore I is true. _____
5. Given A as true, therefore I is undetermined. _____
6. Given E as false, therefore I is undetermined. _____
7. Given I as false, therefore O is undetermined. _____
8. Given O as true, therefore I is undetermined. _____
9. Given E as false, therefore A could be false. _____
10. Given I as true, therefore O could be true. _____
11. Given All X are Y as false, therefore No X are Y is true. _____
12. Given No A are B as true, therefore All A are B is false. _____
13. Given Some A are B as true, therefore No A are B is false. _____
14. Given Some C are not D as false, therefore Some C are D is true. _____
15. Given All S are P as true, therefore Some S are P is true. _____
16. Given No S are P as false, therefore Some S are not P is false. _____
17. Given Some S are P as false, therefore Some S are not P is true. _____
18. Given No L are M as true, therefore Some L are not M is true. _____
19. Given All L are M as true, therefore Some L are M is true. _____
20. Given Some L are M as true, therefore All L are M is true. _____

101
3.A.3. Exercises: In each of the following sets of statements, if the first statement
(premise) is assumed to be true (T), indicate what can be inferred using the square of the
opposition as the truth-value (True, False or Undetermined) of the subsequent statements.
Then assume the first statement to be false and do the same.
a. All good deeds are deserving of praise. T F
No good deeds are deserving of praise. ____ ____
Some good deeds are deserving of praise. ____ ____
Some good deeds are not deserving of praise. ____ ____
b. No tyrants are just persons. T F
All tyrants are just persons. ____ ____
Some tyrants are just persons. ____ ____
Some tyrants are not just persons. ____ ____
c. Some people are benefactors of humankind. T F
All people are benefactors of humankind. ____ ____
No people are benefactors of humankind. ____ ____
Some people are not benefactors of humankind. ____ ____
d. Some persons are not believers in God. T F
All persons are believers in God. ____ ____
No persons are believers in God. ____ ____
Some persons are believers in God. ____ ____
102
3.A.4. Exercises: Determine whether the following immediate inferences are
valid or invalid.
1. Given as false: Some students are not nice people.
therefore true: Some students are nice people.
2. Given as true: All communists are radicals.
therefore undetermined: Some communists are not radicals.
3. Given as true: Some acts of violence are not justifiable.
therefore undetermined: Some acts of violence are justifiable.
4. Given as false: No believer is an unhappy person.
therefore undetermined: Some believers are not unhappy persons.
5. Given as true: No poor people are happy persons.
therefore false: Some poor people are happy persons.
6. Given as true: All dogs are animals.
therefore true: Some dogs are animals.
7. Given as false: Some planes are jets.
therefore true: Some planes are not jets.

103
8. Given as true: No hero is a coward.
therefore false: All heroes are cowards.
3.A.5. Exercises: What proposition must be shown to be true in order to refute the
following statements:
1. All motorcars are polluters.
2. No Hispanic person is a rich capitalist.
3. All women are poor drivers.
4. Some private enterprises are not enemies of the poor.
5. Some homes for sale are expensive.

104
6. All Republicans are conservative individuals.
7. Some politicians are corrupt officials.
8. Some auto mechanics are not dishonest persons.
9. All fetuses in the womb are human beings.
10. Some nations are not colonizers.
11. All SUV drivers are rude people.
12. Some swans are black.

105
13. No atheist is a moral person.
14. No philosopher is a mathematician.
15. All Europeans are anti-Semitic.
106
3B. Set Theoretic Concepts: Complementation, Venn Diagrams, and Distribution
In Aristotelian logic each statement in ordinary language that is true or false is interpreted
as representing a certain relationship between two classes of things - the class of things
referred to by the subject of the statement and the class of things referred to by the
predicate of the statement. Statements are re-written into standard categorical form in
order to make clear what the subject and predicate terms are and exactly what
relationship is being asserted between them. We have seen that this involves clearly
specifying the subject class S, the predicate class P, the quantity of the subject intended
(universal or particular) and the copula (affirmative or negative).
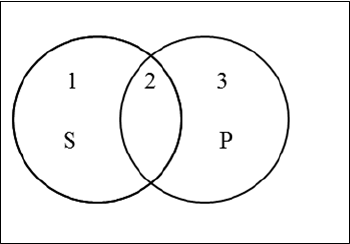
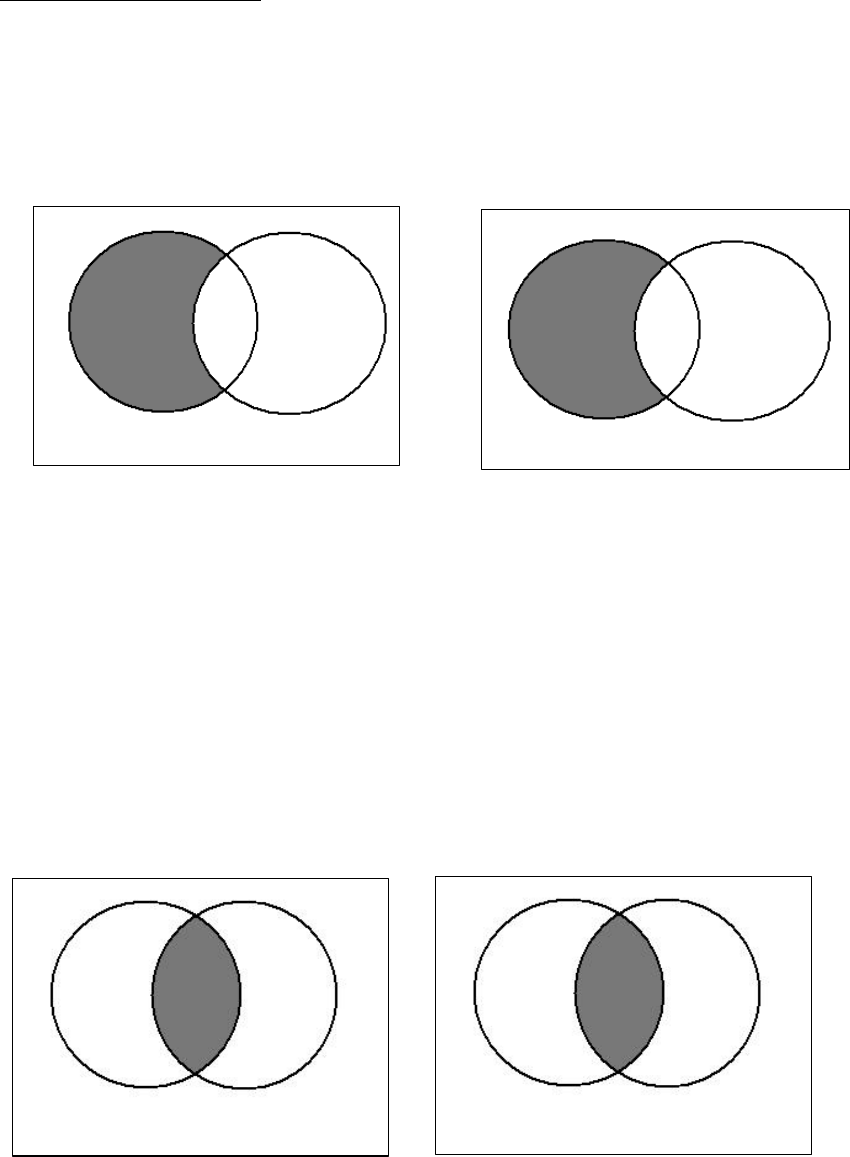
This information can be represented using Venn diagrams. This is done by first drawing
two interlocking circles, the first circle representing the subject class (S) and the second
circle representing the predicate class (P):
Figure 3.16
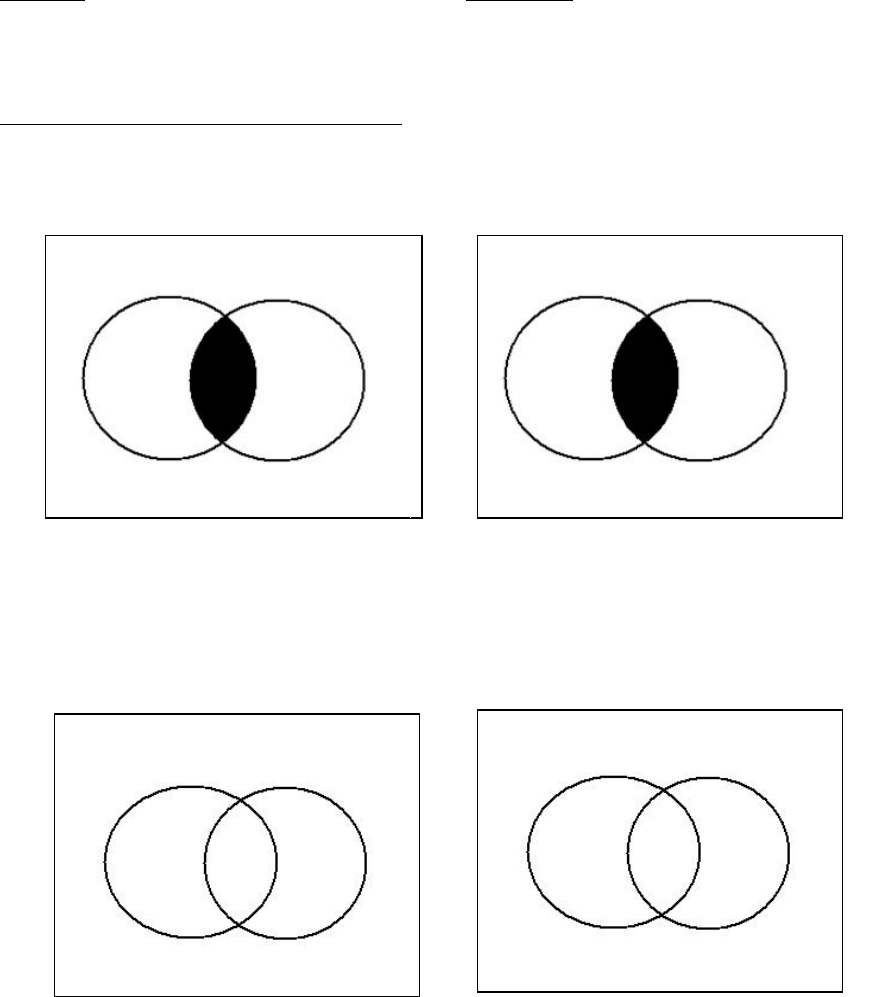
The two interlocking circles have three sections, section 1, section 2, and section 3.
Section 1 is that part of S that does not contain any of P. Section 2 is that part of S that is
also a part of P. And section 3 is that part of P that does not contain any of S. The notion
of the complement of a set is useful here: For any class, K, there is another class called
the complement of K (symbolized as non-K or K*), which consists of all the things in
the universe that are not members of K.
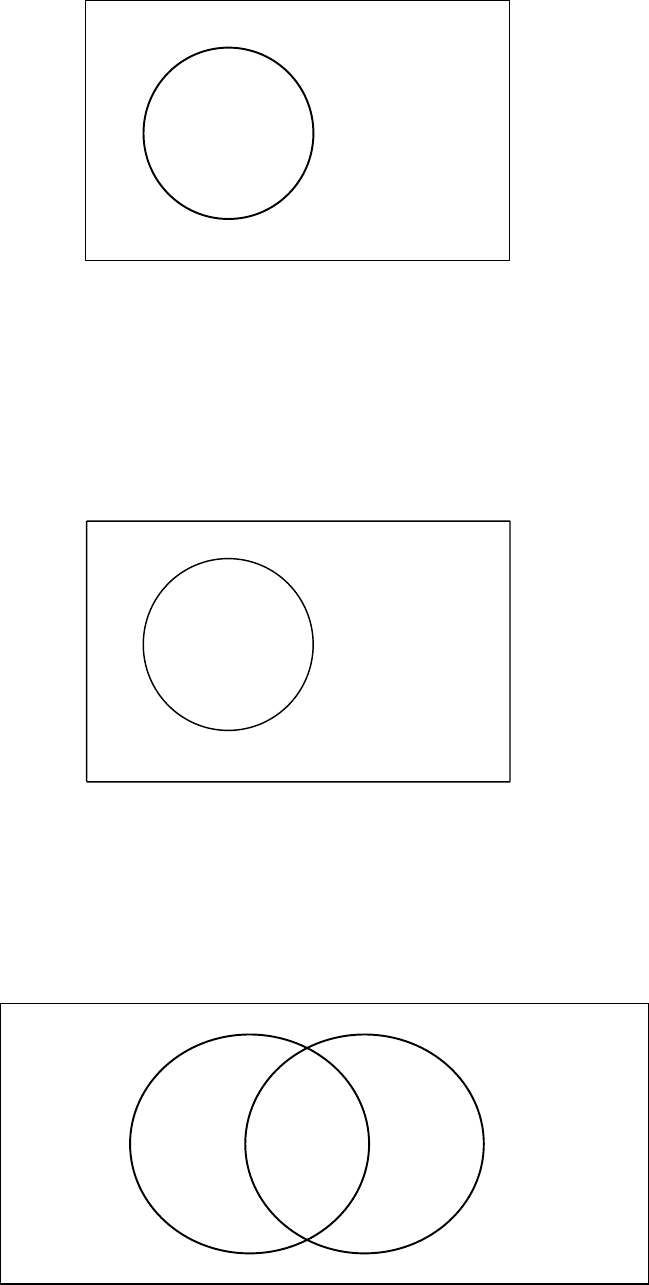
107
Figure 3.17
Thus, if D is the class of dogs then D* would refer to the class of all things which are
non-dogs.
Figure 3.18
We can now describe sections 1, 2, 3 as follows:
Figure 3.19
SP* SP S*P S*P*
D D*
K K*
K*
108
All S*P* is that part of the universe that contains no members of S and no members of P.
SP* is that part of the universe that contains members of S and no members of P.
S*P is that part of the universe that only contains members of P and no members of S.
SP is that part of the universe whose elements are simultaneously members of S and
members of P.
Using these conventions, we can now represent all the propositional forms of categorical
logic in Venn diagram form.
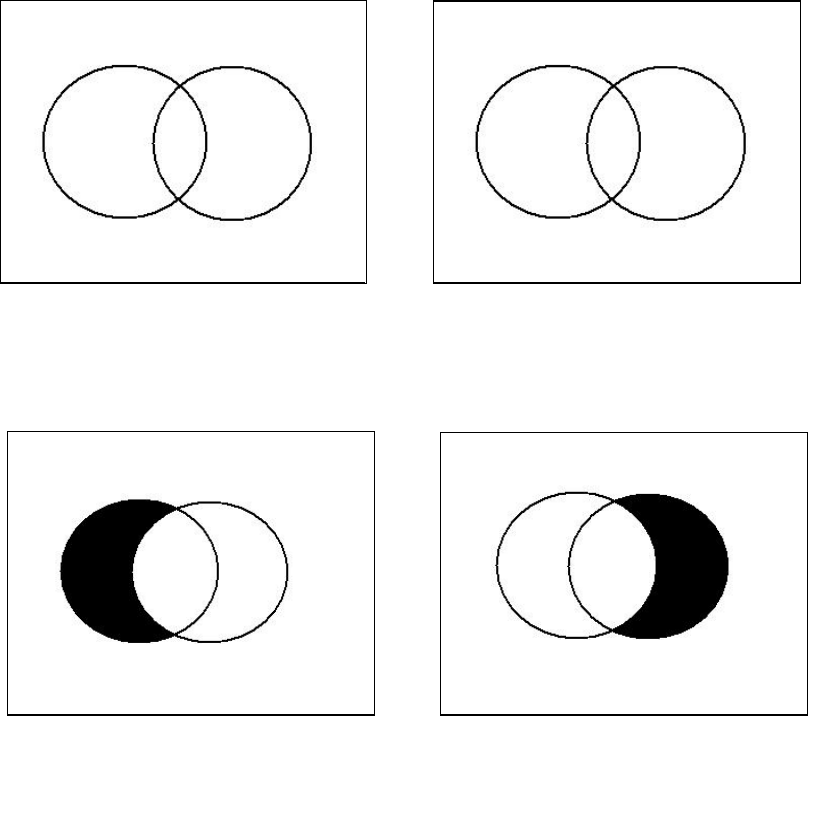
Any statement of the form "All S are P" is asserting that, if there are any members of S,
they cannot be in that part of the universe designated SP*. Rather, they must be in that
part of the universe designated by SP. We adopt the convention of shading in a portion of
the universe to indicate that nothing is in that portion.
Figure 3.20
Any statement of the form “No S are P” is asserting that there are no members of S that
are also members of P. This means that there are no members of SP. SP is empty and we
symbolize this as:
Figure 3.21
S*P*
No S are P.
S*P*
All S are P.
SP
S*P
SP*
S*P
109
In order to symbolize the kind of relationship that holds in particular propositions, we
adopt a second convention, that of putting an X in that portion of the universe in which a
proposition asserts that something exists. Thus, any statement of the form “Some S are P”
is asserting that there is something that is a member both of S and of P. This is
symbolized as:
Figure 3.22
Finally, any statement that has the categorical form of “Some S are not P” is asserting
that there exists something in S that is not a member of P. This is symbolized as:
Figure 3.23
This information is summarized as follows:
S*P*
Some S are P. X
S* P*
Some S are not P. X
110
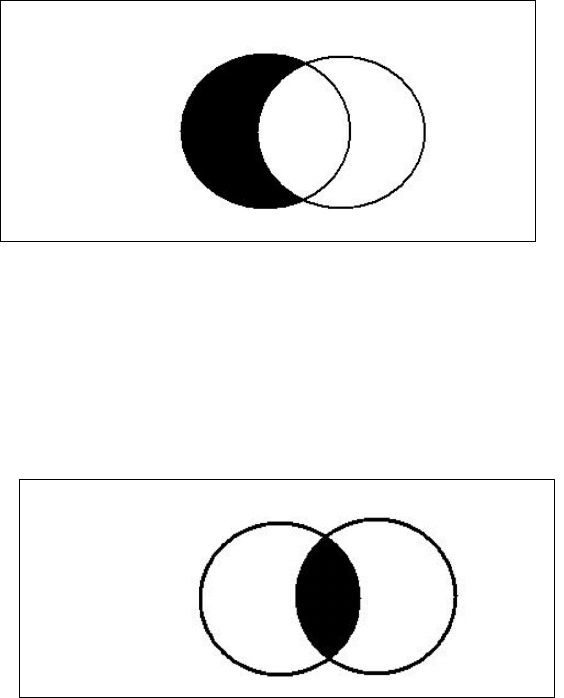
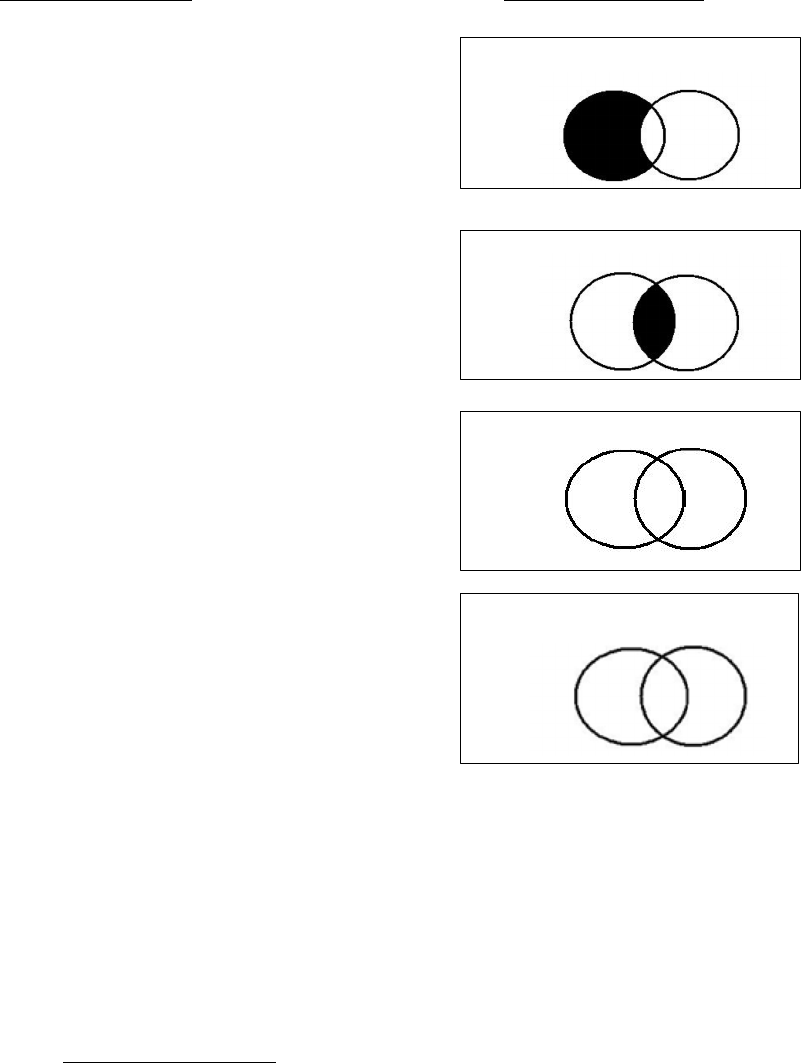
Propositional Form Venn Diagram Form
E: No S are P
I: Some S are P
O: Some S are not P
We classify statements as having a universal or particular propositional form depending
on the quantity of the subject class intended. Thus, statements having an A or E form are
called universal propositions because they relate every member of the subject class to the
predicate class; in an A proposition, every member of the subject is included in the
predicate class, while in an E proposition every member of the subject class is excluded
from the predicate class.
A: All S are P
S*P*
S P
S* P*
X
S*P*
S*P*
X

111
Likewise, statements having an I or O propositional form are called particular
propositions because they relate only some of the members of that subject class to the
predicate class: in an I proposition, part of S is included in part of P; while in an O
proposition part of S is excluded from all of P.
While we will continue to classify the form of a statement as universal or particular based
on the quantity of the subject class intended, we can nonetheless talk about the quantity
of the predicate class that is being related to the subject class. Thus, in an A proposition
(“All S are P”), while we are saying something about every member of S, we are not
saying something about every member of P. While it is true that all dogs are animals
(“All D are A”), it is false that all animals are dogs (“All A are D”), rather, only some
animals are dogs (“Some A are D”). In general, if all members of S are included in the
class of Ps, we can only conclude from this that some of P is S. Thus, in an A
proposition, the quantity of the subject is universal and the quantity of the predicate is
particular.
In a statement having an E propositional form (“No S are P”), we are excluding all
members of S from being members of P. And we are excluding all members of P from
being members of S. In this case, the subject class is universal and the predicate class is
universal. Thus, if “No cats are dogs” is true, then “No dogs are cats” is equally true.
In a statement having an I propositional form (“Some S are P”), part of the subject class
is included in the predicate class and part of the predicate class is included in the subject
class. Thus, both the subject and the predicate class are particular. Finally, in a statement
having an O propositional form (“Some S are not P”) part of the subject class is being
excluded from all of the predicate class. The O proposition says something about every
member of the predicate class, namely that there is at least one member of the subject
class that is distinct from every member of the predicate class. Thus, the quantity of the
subject class is particular and the quantity of the predicate class is universal.
112
The following table summarizes the quantity of the subject and predicate terms for each
of the propositional forms of Aristotelian logic:
A: All S (universal) are P (particular)
E: No S (universal) are P (universal)
I: Some S (particular) are P (particular)
O: Some S (particular) are not P (universal)
A term is distributed in a proposition if its quantity in that proposition is universal. A
term is undistributed in a proposition if its quantity in that proposition is particular. The
following table tells us, for each of the A, E, I, and O propositional whether its subject
(S) or its predicate (P) is distributed or undistributed.
Distributed Undistributed
A S P
E S, P
I S, P
O P S
3.B.1. Exercises:
Give the Venn Diagram representation of each of the following propositions and indicate
whether the subject and predicate are distributed (D) or undistributed (Und.).
1. No elephant is beautiful.
2. Some candies are fattening.
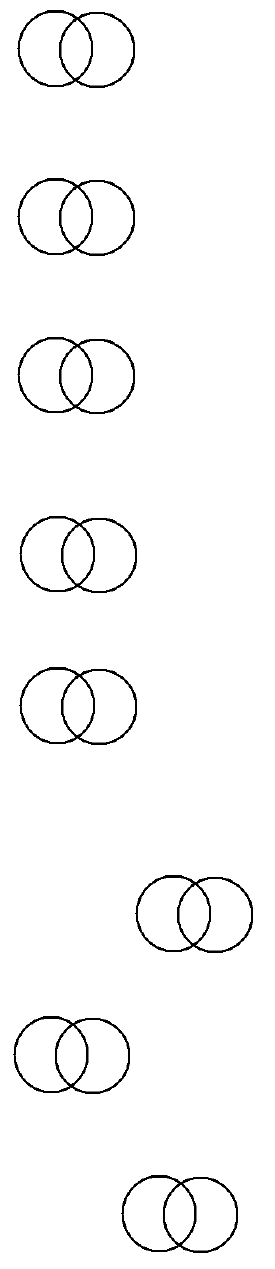
113
3. All candies are fattening.
4. Some books are not enlightening.
5. No incubators are cold.
6. Some important news is depressing.
7. All elevators are round.
8. Some independent farmers are not bankrupt.
9. All rugs are hand-woven.
10. Some dogs are animals that are not large.

114
Obversion and Conversion
Two kinds of immediate inferences often occur in everyday life. They are formally
called obversion and conversion.
To illustrate, take the following situation: A, B and C are discussing the economic
situation. A complains to B: “Many poor people are unemployed.” C, who is hard of
hearing, asks B to repeat what A said. So, B tells C that A said “Many poor people are
not employed.” But A immediately objects and tells B that that is not what A had said. A
then repeats the original statement “Many poor people are unemployed.” B insists that
this says the same thing. Who is right, A or B?
Take another example where A is arguing with B.
A: “I maintain that all communists are radicals.”
B: “I don't agree. I don't believe that all radicals are communists.”
A: “But I didn't say that.”
B: “Well, it's the same thing.”
Is B correct in her contention that “All communists are radicals” means the same thing as
“All radicals are communists”?
The first example illustrates the immediate inference called obversion. The second
illustrates the immediate inference called conversion.
C. OBVERSION
Obversion is the process of constructing an equivalent statement from a premise in such a
way that the quantity and subject of the premise remains the same while the quality and
the predicate are changed to their opposites.

115
Premise: All voters are citizens.
All people who are voters are people who are citizens.
Obverse: No voters are non- citizens.
No people who are voters are people who are not citizens.
In the obverse, the quantity of the original statement remains universal and the subject is
voters, but the quality and predicate has changed. In the original statement, the quality of
the proposition was affirmative. In the obverse statement, it is negative and the predicate
of the original statement is replaced by its complement. But the original meaning has not
changed.
Premise: Some citizens are voters.
Obverse: Some citizens are not non-voters.
Some citizens are not people who are not voters.
Obversion shows how one and the same idea can be expressed either affirmatively or
negatively.
3C.1. Exercises:
See if you can determine whether the B statement has the same meaning as the A
statement in the following examples.
A B
1. All women are females. No women are people who are not females.
2. No men are females. All men are people who are males.
3. Some cities are overcrowded. Some cities are not overcrowded.
4. Some workers are not employed. Some workers are employed.
5. Some students are religious. Some students are not people who are not
religious.

116
C.II. Terminology
Following are some preliminary terms used in the obverse operation:
Obvertend - the premise of an immediate inference by obversion.
Obverse - the conclusion.
Complement of class A - all things that are not A.
Thus, the complement of the class “citizens” is the class of ‘things that are not
citizens’, or the class of non-citizens. The complement of the class “animal” is
“non-animal” and is the class of ‘things that are not animals’, such as plants and
stones. However, the complement of the class “heroes” is not the class “cowards”
but the class of persons that are not heroes or “non-heroes.” For persons who are
not heroes are not necessarily cowards. If we use the symbol S to denote the
subject class, then the complement of S is non-S. And the complement of non-S is
non-non S, or simply S. Accordingly, the complement of the class of non-voters is
simply the class of voters.
Using the terms obvertend, obverse, and complement, the rules of obversion are
as follows.
C.III. Rules of Obversion
Rule 1. The subject term of the obvertend and its quantity remains unchanged.
Rule 2. Change the copula quality of the obvertend.
Rule 3. Replace the predicate term of the obvertend by its complement.
We can illustrate the rules by the following example:
117
Obvertend: All patriots are heroes. (A proposition)
All people who are patriots are people who are heroes.
Obverse: No patriots are non-heroes. (E proposition)
No people who are patriots are people who are not heroes.
Notice that the subject term “patriots” remains unchanged in meaning and in quantity in
the obverse. The quantifier “No” has a double function. It keeps the original quantity of
the S term universal, but it also changes the quality of the original statement (the
obvertend) from affirmative to negative. Thus, the original A proposition has become an
E proposition. Lastly, observe that the predicate term of the obvertend has been replaced
by its complement, non-P (non-heroes). From the original proposition, “All patriots are
heroes," we have immediately inferred another proposition, “No patriots are non-heroes,”
which is equivalent in meaning to the first one.
We can also show by means of the two-circle Venn diagram that the obvertend “All S is
P” is equivalent in meaning to its obverse “No S is non-P.” Thus, we have
Figure 3.24
Because the diagrams are identical, the meaning of the two statements is the same.
=
S*P*
SP* SP
All S is P.
S*P*
SP* SP
No S is P*.
S*P
S*P
118
C.IV. Kinds of Obversion
An A statement obverts to an E.
(A) All S is P
(E) No S is P*
Fig. 3.25
An E statement obverts to an A.
(E) No S is P
(A) All S is P*.
Figure 3.26
=
=
S*P*
SP* SP S*P
No S is P.
S*P*
SP* SP S*P
All S is non-P.
S*P*
SP* SP
All S is P.
S*P*
SP* SP
No S is P*.
All S is P*.
S*P
S*P
119
An I statement obverts to an O.
(I) Some S is P.
(O) Some S is not P*.
Figure 3.27
An O statement obverts to an I statement.
(O) Some S is not P.
(I) Some S is P*.
Figure 3.28
Some S is P.
=
=
S*P*
S*P*
X
Some S is not P*
X
X
X
SP
SP
S*P*
S*P*
SP*
S*P
SP*
S*P
Some S is not P
Some S is P*

120
3.C.2. Exercises:
Obvert the following:
1. All S is P*. __________________________________
2. No S is P* __________________________________
3. Some S* is P*. __________________________________
4. Some S is not P*. __________________________________
5. All X is Y. __________________________________
6. No L is M*. __________________________________
7. Some R is S*. __________________________________
8. All gold is metal. __________________________________
9. No dog is an invertebrate. __________________________________
10. Some mistakes are avoidable. ____________________________
3.C.3. Exercises: Determine whether the following are valid obversions:
1. Some women are mothers.
Some women are not mothers.
2. Some men are bachelors.
Some men are not non-bachelors.
121
3. All effects are caused.
No effects are uncaused.
4. Some workers are union members.
Some workers are not union members.
5. All heroes are courageous.
No heroes are cowards.
6. No illiterate person is educated.
All illiterate persons are uneducated.
7. All oppressors are inhumane.
No oppressors are humane
8. Most scientists are non-philosophers.
Most scientists are not philosophers.
9. Some cigarettes are not filtered.
Some cigarettes are unfiltered.
10. No poor person is wealthy.
All poor persons are persons who are not wealthy .
11. Some scientists are prejudiced.
Some scientists are not prejudiced.
12. Mary admires Jane.
Mary is not a person who does not admire Jane.

122
13. Some good people are not people who are religious.
Some good people are people who are religious.
14. Some actions are ethical.
Some actions are not unethical.
15. All guests are welcome.
No guests are unwelcome.
3.C.4. Exercises: Translate each of the following into A,E,I, or O propositions, with
subject and predicate in genus-difference form (p.69); then obvert.
1. Every fish is a vertebrate.
________________________________________
2. Some animals are intelligent.
_________________________________________
3. Every mammal is warm-blooded.
_________________________________________
4. Some drinks are intoxicating.
__________________________________________
5. Every non-Aryan is non-inferior.
__________________________________________
6. No fish are unable to swim.
7. No war is without harm to the innocent.
___________________________________________

123
8. No education is inexpensive.
____________________________________________
9. All indigent families are without resources.
____________________________________________
10. Many workers are unemployed.
____________________________________________
11. All people who are not registered are non-students.
____________________________________________
12. Some non-Communists are not non-conservatives.
3.C.5. Exercise: For each statement below, circle the letter of the obverse.
1. Some government officials are not people who are not clear about morality
a. Some government officials are people who are not clear about morality
b. Some government officials are not people who are people who are clear
about morality.
c. Some people who are government officials are people who are not clear
about morality.
d. Some government officials are people who are clear about morality
e. Some people who are government officials are not people who are clear
about morality.
124
2. All people who are not poor are unable to lead productive lives.
a. No people who are not poor are not able to lead productive lives.
b. No people who are poor are able to lead productive lives.
c. No people who are not poor are able to lead productive lives.
d. No people who are poor are non-unable to lead productive lives.
e. No people who are poor are people who are not able to lead
productive lives.
3. Some steelworkers that are not employed are involved in activities that
are interesting.
a. Some steelworkers that are employed are involved in activities that
are not interesting.
b. Some steelworkers that are not employed are not involved in activities
that are interesting.
c. Some steelworkers that are not employed are not involved in activities
that are not interesting.
d. Some steelworkers that are employed are not involved in activities
that are interesting.
e. Some steelworkers that are employed are not involved in activities
that are not interesting.
4. No people who are in love are able to ignore a beautiful sunset.
a. All people who are not in love are able to ignore a beautiful sunset.
b. All people who are not in love are not able to ignore a beautiful
sunset.
c. All people who are not in love are people who are not able to ignore a
beautiful sunset.
d. All people who are in love are unable to ignore a beautiful sunset.
e. All people who are in love are people who are able to ignore a
beautiful sunset.
125
D. CONVERSION
Conversion is the process of drawing an immediate inference or conclusion (called the
converse) from an original statement (called the convertend), by having the subject and
predicate trade places.
Venn Diagram Illustration of Conversion.
E Proposition:
Figure 3.29
I Proposition:
Figure 3.30
No P is S.
=
=
S*P*
S*P*
SP*
S*P
SP*
S*P
No S is P
S*P*
Some S is P
Some P is S
X
X
SP*
S*P
S*P
SP*
126
For E and I propositions, the diagram for the convertend is the same as that for the
converse. Therefore, they are equivalent.
O Proposition:
Figure 3.31
Figure 3.32
≠
SP
S*P*
X
X
Some S is not P
Some P is not S
SP*
S*P
SP*
S*P
All S are P
SP
S*P
SP*
SP
All P are S.
SP
S*P*
S*P*
S*P*
≠

127
Clearly the diagrams of the converse and convertend are not identical in the case of A and
O propositions.
1
Thus the A and O propositions are not equivalent in meaning to their
converses.
VI. Kinds of Conversion
A Proposition:
(A) All S is P All gold is metal.
(A) All P is S All metal is gold.
E Proposition:
(E) No S is P No dog is invertebrate.
(E) No P is S No invertebrate is a dog.
I Proposition :
(I) Some S is P Some men are oppressors.
(I) Some P is S Some oppressors are men.
O proposition:
(O) Some S is not P Some animals are not horses.
(O) Some P is not S Some horses are not animals.
1
We can, however, infer “Some P are S" from "All S are P” if we make the existential assumption that
there exists at least one member of the class S. The resulting converse is limited (from “All S are P” to
"Some P are S") . Hence, it is called a conversion by limitation or per accidens. More on this in the second
part of the chapter.

128
3.D.1. Exercises: Conversion
A. Translate the following statements into Genus-Difference format, convert, and
state whether the converse is equivalent to the convertend.
1. O.J. Simpson played football.
______________________________
2. Some machines are noisy.
_________________________________
3. Most dogs are not red.
____________________________________
4. Many lawyers are unethical.
_____________________________________
5. Christians always love one another.
______________________________________
6. Some advocates are needed in impoverished communities.
_________________________________________________
7. All fish swim.
_______________________________________________
8. Some plants are not edible.
________________________________________________
9. No happy man is sad.
________________________________________________
10. Most educated people succeed in life.
_________________________________________________

129
11. Honesty is never the best policy.
________________________________________________
12. All men are organisms.
________________________________________________
13. All communists hate capitalism.
__________________________________________________
14. Some students who do not study fail their exams.
__________________________________________________
3. D.2 Exercises:
B. Determine whether the following immediate inferences are valid (V) or
invalid (I).
_____1. Some detectives are not policemen, therefore, some policemen
are not detectives.
____ 2. All animals are mobile, therefore, all mobile things are animals.
____ 3. Most politicians are corruptible, therefore, some corruptible
people are politicians.
____ 4. All mammals are warm-blooded animals, therefore, all warm-blooded
animals are mammals.
____ 5. All men die, thus some things that die are men.
____ 6. Some witnesses do not tell the truth, therefore, some people who do not
tell the truth are witnesses.
_____ 7. No plant has sense organs, therefore, no possessors of
sense organs are plants.
_____ 8. Some rich people are unhappy, therefore, some unhappy people
are rich.
130
_____ 9. Some defeats are not embarrassing, therefore, some embarrassing
things are not defeats.
_____ 10. Every dishonest person is untrustworthy, therefore, every
untrustworthy person is dishonest.
_____ 11.We can infer that some retired workers are elderly people,
since some elderly people are retired workers.
_____ 12. If no stones are living, we can infer immediately that no
living thing is a stone.
_____ 13. It is correct to infer that some workers are users of public
transportation from the fact that some users of public
transportation are workers.

131
3. D.3. Exercises: For each statement below, circle the letter of the equivalent converse.
If there is no equivalent converse, circle the letter indicating “none.”
1) No man is able to live without a challenge.
a) All men are able to live with a challenge.
b) Some men are able to live with a challenge.
c) All people who are able to live without a challenge are not men.
d) No people who are able to live without a challenge are men.
e) None.
2) Some cats are stronger than dogs.
a) Some cats are not stronger than dogs.
b) Some things stronger than dogs are cats.
c) Some dogs are stronger than cats.
d) Some things stronger than dogs are not things stronger than cats.
e) None.
3) Some tall men are not short.
a. Some men who are short are not tall
b. Some men who are tall are men who are not short.
c. Some men who are not short are not men who are tall.
d. Some men who are not short are men who are not tall.
e. None.
4) All chairs are made for rough treatment.
a. All things made for rough treatment are chairs.
b. Some things made are chairs for rough treatment
c. All things that are chairs are things not made for rough treatment.
d. Some things made for rough treatment are chairs.
e. None.
132
E. Contraposition
We form the contrapositive of a statement by replacing its subject with the compliment of
its predicate and replacing its predicate with the compliment of its subject. Thus we
have:
Original Contrapositive
All S is P All P* is S*
No S is P No P* is S*
Some S is P Some P* is S*
Some S is not P Some P* is not S*
In each of these cases, the contrapositive is derived from the original statement by a
series of immediate inferences:
Statement 1: the original statement
Statement 2: obverse of statement 1
Statement 3: converse of statement 2
Statement 4: obverse of statement 3 = the contrapositive of the original
Original obverse converse obverse
All A are B No A are B* No B* are A All B* are A*
No A are B All A are B* All B* are A No B* are A*
Some Aare B Some A are not B* Some B* are not A Some B* are A*
Some A are not B Some A are B* Some B* are A Some B* are not A*

133
While the obverse operation always gives a statement of equivalent truth value, the
converse operation does not. In deriving the contrapositive of both the E and I
propositional forms, the conversion operation is not a valid inference and does not
necessarily produce an equivalent propositional form. But for the A and O forms, if ‘All
A are B’ is true, then ‘All B* are A*’ is true; and if ‘Some A are not B’ is true, then
‘Some B* are not A*’ is true.
The operations of obversion, conversion, and contraposition allow us to say simple things
in complex ways. It also helps us to decipher complex language and reveal hidden
meaning.
3.E.1. Exercises: Write out the contrapositive of each of the following statements:
1) All mammals are animals.
2) Some animals are not mammals.
3) Some mammals are not animals.
4) Some mammals are things that are not animals.
5) No things that are not mammals are animals.
6) All things that are not mammals are things that are not animals.
7) All things that are not animals are things that are not mammals.
8) No mammals are thing that are not animals.
9) Some animals are things that are not mammals.

134
10) Some things that are not mammals are not things that are not animals.
3.E.2. Exercises: Determine which of the following are valid arguments:
1) All dogs are things that are not cats. Therefore, all cats are things that are not
dogs.
2) No dogs are things that are not cats. Therefore, no cats are things that are not
dogs.
3) Some things that are dogs are cats. Therefore, some things that are cats are dogs.
4) Some dogs are things that are not cats. Therefore, some cats are things that are not
dogs.
5) Some things that are not cats are things that are not dogs. Therefore, some dogs
are cats.

135
F. CATEGORICAL SYLLOGISMS
In this part of the chapter, we will consider arguments involving mediate inference,
where there is more than one premise. The classic example of mediate inference is the
categorical syllogism. A syllogism is a deductive argument in which a conclusion is
inferred from two premises. A categorical syllogism is a deductive argument in which the
conclusion and the two premises are all categorical propositions.
Introduction
In everyday life, constant use is made of the categorical syllogism. We can illustrate its
use in the current discussion on the justification of preferential treatment for women and
other groups that have been historically denied opportunities.
A: I say that women deserve preferential treatment
because they have been exploited and discriminated against. All
exploited people have a right to compensation, and preferential
treatment is a form of compensation for historical and current injustice.
B: I disagree with your position. I maintain that preferential
treatment is unfair. All awarding of jobs and educational
opportunities should be based on merit alone.
A: How can you talk of fair competition for jobs and education based
on merit when women have been and continue to be denied opportunities
available to men? There is no fairness in merit alone when women
have been systematically disadvantaged relative to men.
136
B: But if you give preference to those who are incompetent, then
the quality of goods and services will be lowered. You don't want an
incompetent doctor treating you, just because some bureaucrat had to fill a
quota.
A: I deny your premise that preferential treatment rewards incompetents.
Preferential treatment means that among all those found competent,
women should be given preference. It does not follow that the quality of
goods and services will be lowered.
Let us now formalize the syllogisms contained in the foregoing discussion:
A: All people who have been historically exploited have a right to be
compensated.
All women have been historically exploited.
All women have a right to compensation.
Some forms of preferential treatment are forms of compensation.
Some form of compensation is deserved by women.
Some form of preferential treatment is deserved by women.
B: All awarding of jobs and educational slots on the basis
of merit is fair competition.
Preferential treatment does not award jobs and educational
slots on the basis of merit.
Preferential treatment is not fair competition.
137
A: Some educationally disadvantaged peoples are unable to
compete on the basis of merit alone.
Some women are educationally disadvantaged
people.
Some women are unable to compete on the basis
of merit alone.
B: All cases where employment and educational slots are awarded
through preferential treatment are cases that lower the quality of
goods and services in the country.
Preferential treatment awards jobs and educational slots to less competent
people.
Preferential treatment lowers the quality of education and
services in the country.
A: Awarding employment and educational slots to competent
women over competent men does not lower the quality of education and
services in the country.
Preferential treatment awards jobs and educational slots to
competent women over competent men.
Preferential treatment does not lower the quality of education
and services in the country.
Of course, most people do not normally argue in the formal way shown above. In
normal discussions, the conclusion sometimes appears first and, then, the reasons or
premises to support the conclusion follow. This is the case in A's first argument. Again,
in everyday arguments, sometimes not all the premises are explicitly mentioned. It is left
to the listener to furnish the missing premise. This is the case in B's first argument.

138
In order to analyze an argument, all the premises should be explicitly stated and the
conclusion placed last. In this section, we will explore not only how to put syllogisms
into this standard form, but more importantly, how to distinguish valid from invalid
syllogisms.
I. The Structure of the Categorical Syllogism
The standard form of a categorical syllogism has (1) three propositions, and (2) three
terms.
The three propositions are:
1. The major premise
2. The minor premise
3. The conclusion
The three terms are:
1. The major term P
2. The minor term S
3. The middle term M
Consider the following example of a categorical syllogism:
All animals are organisms.
All bears are animals.
Therefore, all bears are organisms.

139
II. Terms: The first step in evaluating any argument is identifying its conclusion.
From our earlier study of distinguishing premises from conclusions, we know that the
word “therefore” is a conclusion indicator. Thus, the last statement in the syllogism is the
conclusion, and the major term is the predicate term, P, of the conclusion. In the
syllogism given, the term “organisms” is the major term of the syllogism.
The minor term is the subject term, S, of the conclusion. In this case, it is the term
“bear.” The predicate term of the conclusion is called the major term because the
predicate of a proposition is usually wider in extension than the subject term. Thus, the
predicate term, “organisms,” is wider in scope than the subject term, “bear.”
The middle term is the term, M, that appears only in the premises and connects the
major and minor terms. In this case, it is the term “animals.”
III. Premises:
The major premise is the premise that contains the major term. In this case, the major
premise is “All animals are organisms.”
The minor premise is the premise that contains the minor term. In this case, the minor
premise is “All bears are animals.”
In a standard-form categorical syllogism, the major premise must come first, next, the
minor premise, and lastly, the conclusion. The example above thus has the following
structure:
All animals (M) are organisms (P). (Major premise)
All bears (S) are animals (M). (Minor premise)
All bears (S) are organisms (P). (Conclusion)
In a lateral format, this would be written:
All M are P. / All S are M. // All S are P.
140
Observe that each term appears twice in the syllogism. The major term (P) appears once
in the conclusion and once in the major premise. The minor term (S) appears once in the
conclusion and once in the minor premise. The middle term (M) appears once in the
major premise and once in the minor premise, but it never appears in the conclusion.
If we eliminate the quantity and the copula and give the skeletal structure alone, then we
have the following figure:
Figure 3.33
IV. Figure and Mood of the Syllogism
The S, P, and M terms can vary their positions in the premises of the syllogism to
produce different arrangements known as figures of the syllogism. There are four
possible figures illustrated as follows:
Figure 1 Figure 2 Figure 3 Figure 4
Major M P P M M P P M
Minor S M S M M S M S
Concl. S P S P S P S P
Figure 3.34

141
3.F.1. Exercises: Determine the figure of the following syllogisms.
(1) All dogs are animals.
All German Shepherds are dogs.
All German Shepherds are animals.
(2) No saints are sinners.
Some men are sinners.
Some men are not saints.
(3) All students are learners.
Some students are children.
Some children are learners.
(4) All leopards are spotted animals.
Some spotted animals are cats.
Some cats are leopards.
(5) All X are Y.
All Z are Y.
All Z are X.
(6) No L are M.
All M are R.
No R are L.
(7) All horses are animals with backbone.
Some mammals are horses.
Some mammals are not animals with backbone.
142
(8) No men are women.
All mothers are women.
No mothers are men.
(9) No winners are losers.
Some losers are gamblers.
Some gamblers are not winners.
(10) All laborers are wage earners.
Some laborers are underpaid people.
Some underpaid people are wage earners.
(11) No Alaskans are Alabamans.
All Alabamans are Southerners.
No Southerners are Alaskans.
(12) Some insects are spiders.
Some animals are insects.
Some animals are spiders.

143
A syllogism is characterized by its figure and also by its mood. By mood we mean the
kind of proposition, A, E, I, or O, that appears as major premise, minor premise and
conclusion. For example, AOI would mean that the major premise is an A proposition,
the minor premise is an O proposition and the conclusion is an I proposition.
The mood and figure of a syllogism can be presented in a box giving the figure of the
syllogism and specifying the form of the major premise, minor premise, and conclusion.
Thus, a syllogism with the form AAA-1 would have the following box form:
A M P
A S M
A S P
3.F.2. Exercises:
Use S, P, and M to write out the syllogistic forms corresponding to the following :
1. AAA-2
2. AAA-3
3. IAO-3
4. EAO-1
5. AII-2
6. OAA-4
144
7. OEO-4
8. EAA-1
9. IAA-3
10. EEE-1
11. OAO-2
12. IEO-1
13. OAI-3
14. EAO-4
15. IAI-2

145
3.F.3. Exercises: Put the following syllogisms into standard form and determine the
mood and figure of each. The steps to follow are:
a. Translate the statements into categorical form if needed.
b. Find the conclusion and locate the subject and predicate
terms so that the major and minor premises can be found.
c. Write the major premise first, next the minor, and finally
the conclusion.
d. Determine the mood and figure.
1. All Nigerians are men because all Nigerians are Africans
and all Africans are men.
2. All guns are dangerous weapons, but no dangerous weapons
are suitable toys for children; consequently, no guns are
suitable for children.
3. No babies are adults, but all adults are full grown; it follows
that no babies are full grown.
4. All things that are oxygen expand when heated because all
things that are oxygen are gases, and all gases expand when
heated.
5. No aircraft carriers are ocean liners, so no warships are
ocean liners since all aircraft carriers are warships.
6. All nuclear missiles are man-made inventions; therefore, some
man-made inventions are not Russian-made inasmuch as some
nuclear missiles are not Russian-made.
7. All oranges are healthy, since everything that contains Vitamin
C is healthy and all oranges contain Vitamin C.
146
8. No economy that exists in mainland China is individualistic, so
no capitalist economy exists in mainland China, since all
capitalist economies are individualistic.
9. No immoral person is a good example to the young, so no child
molesters are good examples to the young, since they are
immoral persons.
10. All theists are believers in God, but no people who are believers
in God are atheists; consequently, no theist is an atheist.
11. All revolutionaries advocate change and so do all enslaved
peoples. Hence, all enslaved peoples are revolutionaries.
12. All people love a winner, but no losers love winners, so no
losers are people.
13. All neurotic children are maladjusted individuals, and some
neurotic children are products of neurotic parents, so some
maladjusted individuals are products of neurotic parents.
14. All human beings are organisms because all human beings are
living, and all living things are organisms.
15. All books of physics are scientific textbooks; but no book of
poetry is a scientific textbook, consequently, no book of physics
is a book of poetry.
16. No scientist is a dumb person because no dumb person is
knowledgeable, and all scientists are knowledgeable.
17. Every scholar is deserving of praise, since every scholar is
hard-working and all hard-working people are deserving of
praise.

147
II. The Rules Method for Testing Validity.
The rules method is not only simple and quick, but that it also gives the specific
fallacy involved in an invalid syllogism. One has to remember only six rules. If a
categorical syllogism does not violate any of these rules, then it is valid, but if even one
rule is violated, then it is invalid. The six rules are as follows:
Rule 1: The middle term must be distributed (universal) in at least one premise.
A violation of Rule 1 commits the fallacy of the undistributed middle
term.
Rule 2: No term can be distributed in the conclusion which is undistributed in the
premise.
A violation of Rule 2 commits either the fallacy of the illicit minor term
or the fallacy of the illicit major term.
Rule 3: No standard form categorical syllogism is valid which
has two negative premises.
A violation of Rule 3 commits the fallacy of exclusive premises.
Rule 4: A negative premise requires a negative conclusion;
a negative conclusion requires a negative premise.
A violation of Rule 4 commits either the fallacy of drawing an
affirmative conclusion from negative premises or the fallacy of drawing
a negative conclusion from affirmative premises.
Rule 5: From two universal premises a particular conclusion
cannot be drawn.
A violation of Rule 5 commits the existential fallacy of assuming a
universal statement is non-empty.

148
Rule 6: A valid syllogism must contain only three terms, each
of which is used in the same sense throughout the argument.
A violation of Rule 6 commits the fallacy of four terms. A specific form
of this fallacy is called the fallacy of the ambiguous middle term.
Rule 1: The middle term must be distributed at least once.
The function of the middle term is to serve as a basis from which we can draw a
conclusion about the relation between the subject and predicate terms of the syllogism. In
order for this to be possible, it must be distributed in either the major premise or the
minor premise. To illustrate, consider the following example:
All horses are animals. (major premise)
All men are animals. (minor premise)
All men are horses. (conclusion)
Recall that a term is distributed if it refers to all members of the class designated by that
term. Otherwise it is undistributed. Thus, the middle term "animal" is undistributed in the
major premise because not all, but only some animals are horses. Similarly, the term
"animal" in the minor premise asserts only that some animals are men. It is invalid to
draw the conclusion that "All men are horses" because that part of the animal class which
refers to horses is not identical with that part of the animal class which refers to men.
A convenient way of detecting violations of Rules 1 and 2 is by the use of the box
method, which illustrates the form of the syllogism. Using the box method for the
syllogism above, the first column determines the mood and the next two columns
determine the figure of the syllogism:

149
Figure 3.43
The following table recounts the distribution of subject and predicate terms for each of
the categorical propositions:
We now determine the quantity (distributed or undistributed) for each term in the
premises and conclusion as follows:
A Pd Mu
A Sd Mu
A Sd Pu
If M is undistributed in both premises, then a violation of Rule 1 occurs, and we have the
fallacy of the undistributed middle term.
Exercises for Rule 1: Determine whether the following syllogisms have a distributed
middle term:
1. Some basic rights are inalienable.
All persons have basic rights.
All persons have inalienable rights.
Quantity of S Quantity of P
___________________________________________________________
A distributed (d) undistributed (u)
E distributed (d) distributed (d)
I undistributed (u) undistributed (u)
O undistributed (u) distributed (d)
150
2. All organisms are cellular.
All animals are cellular.
All animals are organisms.
3. No cars are inexpensive.
Some Chevrolets are cars.
Some Chevrolets are not inexpensive.
4. No As are Bs.
All Cs are As.
No Cs are Bs.
5. No form of slavery is moral.
Some marriages are forms of slavery.
Some marriages are not moral.
6. Some trees are deciduous.
All oaks are trees.
All oaks are deciduous.
7. Most good singers are female.
Ross is a good singer.
Ross is female.

151
8. All poisonous things are dangerous.
All rattlesnakes are poisonous.
All rattlesnakes are dangerous.
9. Many mayors are honest people.
Some town officials are mayors.
Some town officials are honest people.
10. Some gangsters are educated.
Some educated people are not honest.
Some honest people are not gangsters.
Rule 2: No term can be distributed in the conclusion that is not distributed in the
premises.
In essence, this rule states that the conclusion of a valid argument cannot assert more than
is asserted implicitly in the premises. An undistributed term is one that refers to only
some members of a class. One cannot apply to all members of that class what is true of
only a part of it. The following example illustrates a violation of Rule 2:
All cows are females.
All cows are mammals.
All mammals are females.

152
In the minor premise, the S term "mammal" is undistributed, while in the conclusion the
S term is distributed. We can clearly see a violation of the rule using the box method:
3.44
In the minor premise Su translates to "Some S” (Some mammals are cows), while in the
conclusion, Sd translates to "All S" (All mammals are females). To infer more in the
conclusion than what the premise allows is to make an illicit inference; hence, the fallacy
of overextending the S term is called the fallacy of the illicit minor.
The following is an example of an overextension of the major or P term in the
conclusion:
All communists are radicals.
No communists are capitalists.
No capitalists are radicals.
If it is difficult to see the flaw in this argument, the box method will help us see it more
clearly:
3.45
Observe that the major term P in the major premise is undistributed. In other words, it is
making a claim about some radicals. Yet, in the conclusion, we see that the major term P

153
is distributed. It is making a claim about all radicals. The conclusion says more than the
premises allows. The fallacy of overextending the major term P in the conclusion is
called the fallacy of the illicit major.
ii. Exercises for Rule 2.
Examine the following syllogisms for a violation of Rule 2. Name the specific fallacy of
overextension, where applicable.
1. All poodles are domestic animals.
All poodles are dogs.
All dogs are domestic animals.
2. All Republicans are supporters of business.
No Republicans are supporters of labor.
No supporters of labor are supporters of business.
3. Some philosophy courses are interesting.
Some college courses are not interesting.
Some college courses are not philosophy courses.
4. All men who understand children make good fathers.
No men who understand children are impatient.
No impatient men make good fathers.
5. All criminal acts are illegal.
All criminal acts are wicked deeds.
All wicked deeds are illegal.

154
iii. Exercises for Rules 1 and 2:
Determine whether there is a violation of rules 1 or 2 in the following syllogistic forms.
Name the fallacy involved, where applicable.
1. All P is M 2. All M is P 3. All M is P
All S is M All M is S No S is M
All S is P All S is P No S is P
4. All P is M 5. Some P is not M 6. All P is M
Some M is S All S is M Some S is not M
Some S is P Some S is not P Some S is not P
Rule 3: No standard-form categorical syllogism is valid which has two negative premises.
This rule follows naturally from the nature of a syllogism. A syllogism allows us to
determine the relationship between S and P through their respective relationships with M.
If neither S nor P is related to M, we really have no mediation, and hence, no syllogism.
Therefore, from two negative premises, no conclusion can be drawn as to the relationship
between S and P.
Some illustrations may make this clearer:
No gentleman is ill-mannered.
No lady is ill-mannered.
No lady is a gentleman.
The conclusion of this syllogism may be true, but its truth cannot depend on the truth of
the premises used. The subject “lady” and the predicate “gentleman” are both excluded

155
from the class of ill-mannered individuals. Therefore, there is no way to relate the class
of gentleman to the class of ladies. All we can say is that neither a gentleman nor a lady is
ill-mannered, but this tells us nothing about the relationship between ladies and
gentlemen.
To test for a violation of this rule, examine the mood of the syllogism. A violation occurs
if any of the following combinations appear as premises: EE, EO, OE, OO.
Rule 4: A negative premise requires a negative conclusion; a negative conclusion requires
a negative premise.
If both S and P are excluded from M, then we have a violation of Rule 3. If one of the
terms includes M and the other excludes M , then S and P must exclude each other.
Thus, the conclusion must be a negative statement. Consider the following premises:
No males are females.
Some females are politicians.
The only possible valid relationship that could exist between politicians and males is
“Some politicians are not males”. Whenever either premise of a syllogism is negative,
then the conclusion must be negative. Otherwise, we commit the fallacy of drawing an
affirmative conclusion from a negative premise.
Rule 5: From two universal premises a particular conclusion cannot be drawn.
In the Venn diagrams, the particular propositions I and O were diagrammed by placing an
x in the appropriate space. The x implies that there exists at least one member of the class
in which it is placed. Thus, particular propositions are by definition said to have
existential import.
But universal propositions do not always have existential import. That is, they do not
always assert the existence of objects. For example, the statement “All students who fail

156
the test are students who must take a make-up exam” does not imply the existence of
anyone who has or will fail the test. Many universal statements are non-committal about
the existence of members of the subject class S. Given this fact, we cannot claim that
there exists at least one member of S. A violation of Rule 5 is called the existential
fallacy.
2
iv. Exercises for Rules, 3, 4 and 5:
a. Determine whether there is a violation of Rules 3, 4 and/or 5 in the following moods.
Name the fallacy where appropriate.
1. EEO 2. AAE 3. AEO 4. AOI
5. OEO 6. AAI 7. OOO 8. AAA
9. IEO 10. EAO
b. In order to have a valid argument, determine what form, (A, E, I or O), the conclusion
of the following premises should have, if any.
1. AA 2. AE 3. AI 4. AO
5. EA 6. EI 7. IA 8. OA
9. IE 10. IO
Rule 6: A valid syllogism must contain only three terms, each of which is
used in the same sense throughout the argument.
The conclusion of a categorical syllogism asserts a relationship between S and P. This
relationship is justified on the basis of combining premises that assert a relationship
between S and M, and between P and M. If S is related to term M
1
and P is related to
term M
2
, and M
1
≠ M
2
, there is no way that one can use this information to determine the
relationship between S and P.
2
In illustrating immediate inferences (square of opposition, obversion, and
conversion), the assumption was made that S was non-empty. That is, that
there existed some x in S. But in illustrating syllogistic inference, it will not
be assumed that S is non-empty. This will give us practice in using inference
procedures that do and do not make the existential assumption.

157
An example of a violation of Rule 6 is the following:
All men are rational animals.
No women are men.
No women are rational animals.
In this syllogism, the middle term "men" can be used with two meanings. In the major
premise it may be used inclusively, as synonymous with all human beings and would
refer to both males and females. In the minor premise, "men" may be used in an exclusive
sense, referring to the male of the species only. The middle term, therefore, is really two
terms. Thus, we have four terms in the syllogism. A violation of rule 6 is called the
fallacy of four terms. A particular instance of the fallacy of four terms is called the
fallacy of the ambiguous middle, such as the one above. It is not the middle term alone,
however, which can be ambiguous. The S and the P terms can also be ambiguous.
Another instance of the occurrence of four terms involves the collective and divisive use
of a term in the same syllogism. A term is used collectively when it is the predicate of the
subject taken as a group. For example, in “All the angles of a triangle are 180 degrees,”
the term, “180 degrees” is applied to the three angles as a group, not separately. Hence,
the term is used in the collective sense. A term is used divisively when it is the predicate
of the members of the subject class taken individually. Thus, in “All the boys in our
family are college-educated” the predicate, “college-educated” is used divisively, and
applied to each individual separately. The following is an example of a syllogism in
which the middle term is used both collectively and divisively:
Our team played gloriously last night.
Jill King did not play gloriously last night.
Jill King is not a member of our team.
158
The middle term “played gloriously last night” is applied to the team taken as a group in
the major premise, while in the minor premise it is applied to one individual player on the
team. In this way, the fallacy of the ambiguous middle term is committed.
An essential condition for a valid syllogism is that there must be only three terms each of
which is used in the same sense throughout the argument. A vague middle term prevents
us from drawing a decisive conclusion. Terms such as "democracy", "free enterprise",
"law and order", "peace", "success", and "freedom", when used in more than one sense in
an argument, often result in a fallacy of four terms. In the chapter on informal fallacies,
other fallacies resulting from the ambiguity of terms and statements will be discussed.
v. Exercises for Rule 6:
1. The end of life is happiness.
Death is the end of life.
Therefore, death is happiness.
2. To live according to nature is good.
Every man that steals lives according to his nature.
Therefore, every man that steals is good.
3. Mother is a six-letter word.
Mary is a mother.
Therefore, Mary is a six-letter word.
4. All cardinals are birds.
Stan Musial was a Cardinal.
Stan Musial was a bird.
159
5. Nothing is better than God.
But something is better than nothing.
Therefore, something is better than God.
6. Every Liberal is loyal to his party.
But anyone who is broad-minded is a liberal.
So, anyone who is broad-minded is loyal to his party.
7. Everything fast is soon gone.
This color is fast.
Therefore, this color is soon gone.
8. All who know how to drive know how to start a car.
All good golfers know how to drive.
So, all good golfers know how to start a car.
9. Every lion is a feline.
Jai Kel was the lion of Cudah.
So, Jai Kel was a feline.
10. All criminal actions are punishable by law.
All libel suits are criminal actions.
Therefore, all libel suits are punishable by law.
160
vi. Exercises on all Rules:
Translate into categorical form, if necessary, then test the syllogisms for
validity by the use of the Rules Method.
1. All judges are lawyers.
Some African Americans are not judges.
Some African Americans are not lawyers.
2. All good leaders are practicers of what they preach.
Many elected officials are not practicers of what they preach.
Many elected officials are good leaders.
3. Many government officials lack credibility.
No truthful man lacks credibility.
No truthful man is a government official.
4. All efforts to end a war are praiseworthy.
All military orders to massacre civilians are efforts to end a war.
All military orders to massacre civilians are praiseworthy.
5. No radicals are non-violent.
Some revolutionaries are radicals.
Some revolutionaries are non-violent.
161
6. All big stockholders oppose increased corporate taxes.
All who oppose increased corporate taxes are rich people.
All rich people are big stockholders.
7. Most Republicans are pro-business.
Most pro-business people are rich.
Most rich people are Republicans.
8. No addictive drugs can be bought without a doctor's prescription.
Some drugs can be bought without a doctor's prescription.
Some drugs are not addictive.
9. All free countries are true democracies.
No totalitarian states are free countries,
No totalitarian states are true democracies.
10. Many good typists are good stenographers.
Every good secretary is a good typist.
So, every good secretary is a good stenographer.
11. All diamonds are stones.
All diamonds are precious.
Some precious things are stones.
162
12. No glass is a good conductor of electricity.
All glass is non-metal.
No non-metal is a good conductor of electricity.
13. Many teachers have college degrees.
Many educators are teachers.
Many educators have college degrees.
14. No designing person is trustworthy.
All city planners are designing persons.
No city planners are trustworthy.
15. All who understand the young are young.
No old people are young.
No old people understand the young.
16. No babies can reason.
No one who does not know logic can reason.
Thus, anyone who doesn't know logic is a baby.
17. No men are perfect.
No dogs are men.
Therefore, no dogs are perfect.

163
18. Some men make good husbands.
All men are imperfect.
Some imperfect beings do not make good husbands.
19. No government that is divided can stand.
The U. S, government is divided (into legislative, judicial and executive branches.)
So, the U.S. government cannot stand.
20. All members of our club donated a thousand dollars to charity,
Peter is a member of our club.
So, Peter donated a thousand dollars to charity.
3.G.3. Exercises: Name the rules broken and the fallacies committed by the
following invalid syllogisms:
1. AAA-3 2. AAA-2
3. AII-2 4. EAA-1
5. EAO-4 6. EAO-1
7. EEE-1 8. IAO-3
9. IAI-2 10. IEO-1
11. IAA-3 12. OEO-4
13. OAA-4 14. OAI-3
15. OAO-2
164
I. The Venn Diagram Method for Testing Validity
A syllogism is valid if the conclusion necessarily follows from the premises. The three-
circle Venn diagram offers us a technique that proves whether the conclusion necessarily
follows from the premises, or not. This technique involves combining the Venn diagram
of the premises in such a manner as to implicate the Venn diagram of the conclusion. A
syllogism is valid if the Venn diagram of the conclusion is contained in the combined
Venn diagrams of the premises.
Let us proceed to explain the Venn diagram technique of determining validity. In a
previous chapter we introduced the two-circle Venn diagram that showed the class
inclusion or exclusion of two terms, S and P. In a syllogism, however, we have three
terms, S, P, and M. Consequently, we need three overlapping circles as shown below:
3.35
S, P, M refer to the subject, predicate, and middle terms respectively.
S*, P*, and M* refer to the compliments of S, P, and R respectively. The eight different
classes defined by the three-circle Venn are:
S*P*M*
1 2 3
SP*M* SPM* S*PM*
5
4 SPM 6
SP*M S*PM
7
S*P*M
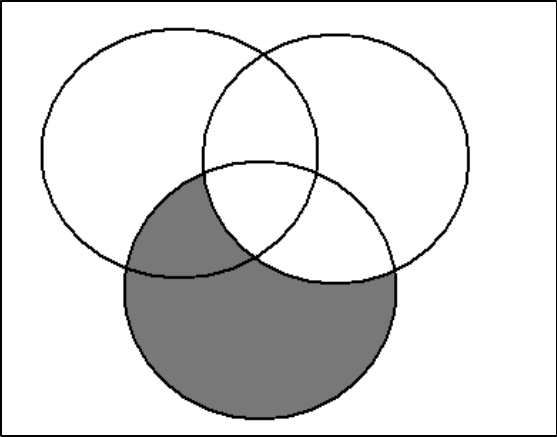
165
1. SP*M* = those S which are neither P nor M.
2. SPM* = those S which are P but not M.
3. S*PM* = those P which are neither S nor M.
4. SP*M = those M which are S but not P.
5. SPM = those S which are both P and M.
6. S*PM = those P which are M but not S.
7. S*P*M = those M which are neither S nor P.
8.
S*P*M*
= those that are neither S nor P nor M.
Exercise: name individuals in the above eight classes where:
S = Americans, British, Asian, Hispanic
P = singers athletes, scientists, politicians
M = females, males
Let us now practice diagramming premises into the three-circle Venn diagram. The
diagram for the universal premise All M is P is:
Figure 3.36
1 2 3
S 5 P
4 PM 6
P*M PM
7
P*M
M
S*P*M*
166
Notice that there are four sections of the circle M. Sections 5 and 6 are M which are P,
while sections 4 and 7 are M which are not P. We must shade in sections 4 and 7 to show
that all M are P. In other words, "M outside P is empty", and is symbolized as MP* = Ø.
Let us next diagram a particular premise: "Some S is M."
Figure 3.37
1 2 3
4 X 5 6
7
S*P*M*
S
P
M
167
Observe in Figure 1 that SM pertains to both sections 4 and 5. Section 4 is in SM which,
however, is not a P, while section 5 is an SM which is also a P. The statement, “Some S
is M” does not specify which section is meant; hence, we need to include both sections
and we do so by putting an X on the line dividing them. Thus, “Some S is M” means that
SM is not empty.
When diagramming premises, remember to equate empty with shaded in areas, and not
empty with an x. Remember, also, when you translate that “All M is P” means, M outside
P is empty; “No M is P” means M inside P is empty; and “Some S is not M” means S
outside M is not empty.
We are now ready to diagram the major and minor premises of a syllogism and then
examine whether their combination produces the diagram for the conclusion. Let us begin
with the following syllogism:
All S is M. / All M is P. // All S is P.
In standard form this would be
All M is P. / All S is M. // All S is P
Giving us the mood and figure AAA – 1.
168
We begin by diagramming the premises:
All M is P (Major Premise) – shade 4 & 7
All S is M (Minor Premise) – shade 1 & 2
Figure 3.38
All S is P (Conclusion) – 1 & 4 shaded
By combining the diagrams of the two premises, the diagram of the conclusion follows
necessarily. There is no member of S that is outside P, since areas 1 and 4 are shaded.
Therefore we conclude that "All S is P." follows from the premises cited.
Let us determine whether the diagram of the conclusion is contained in the combined
diagrams of the premises for the following syllogism:
No P is M. – shade 5 & 6
All S is M. – shade 1 & 2
No S is P. – 2 & 5 shaded
S P
1 2 3
4 5 6
7
M
1
2
3
4
6
7
5
S
P
M
S*P*M*
169
Combining the diagrams for the premises produces the diagram of the conclusion.
Figure 3.39
So far we have diagrammed universal premises. Let us now test a syllogism with one
universal premise and one particular premise:
All M is P –shade 4 & 7
Some M is S – x in 4 or 5
Some S is P – x in 2 or 5
Figure 3.40
1 2 3
S 4 5 6 P
7
M
1 2 3
S P
5
4 6
7
M
S*P*M*
S*P*M*
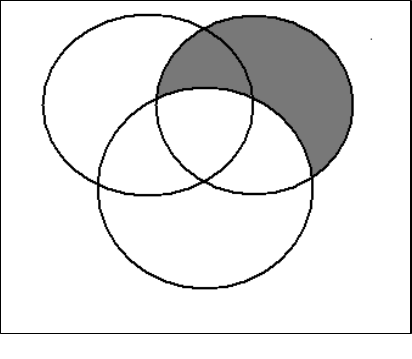
170
We always diagram the universal premise first . This shows us that area 4 has been
shaded out, meaning that it is empty. The second premise, Some M is S, implies that x is
in 4 or 5. But since 4 is empty, the x must be in 5. By combining the diagrams for the
premises, the diagram for the conclusion is automatically produced. Therefore, the
syllogism is valid.
A syllogism involving the insertion of an x is the following:
All P is M shade 2 and 3
Some M is not S x between 6 and 7
Some S is not P x in 1 or 4
As always, we diagram the universal premise first :
Figure 3.41
S P
1 2 3
4 5 6
7
M
1 2 3
S P
5
4 6
7
M
S*P*M*
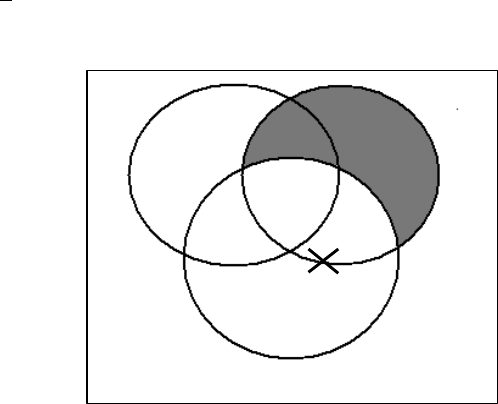
171
Next we diagram the minor premise, “Some M is not S.” Recall that this statement
means that the intersection of S*M is not empty. But S*M has two areas: 6 and 7. We
place an x on the line between them in order to indicate that it is in either 6 or 7. Thus, we
have:
Figure 3.42
Looking at the completed diagram, we see that the conclusion, "Some S is not P" is not
contained in the premises as diagrammed, for there is no x in area 1 or 4.
3.G.1. Exercises: Determine the validity of the following syllogistic forms by means of
the Venn diagrams.
1. AII-2 6. OAO-4 11.AOO-2
2. AAA-3 7. OEO-4 12. IEO-1
3. IAI-3 8. EAE-2 13. OAO-3
4. EAO-1 9. IAA-3 14. EAO-4
5. AAA-1 10. EEE-1 15. IAI-2
1 2 3
S P
4 5 6
7
M
S*P*M*

172
H. Existential Import
In section D of chapter 2 Venn diagrams were introduced in such a way that the Venn
diagram for the A and E propositions did not contain an x. This means that the truth of :
“All S is P” does not necessarily lead to the truth of “Some S is P”. One important reason
for this is the fact that there are many true propositions that do not presuppose the
existence of members of their subject class. An example is the following: "All mermaids
are half-fish”. This proposition does not assert that there are mermaids which have the
property of being half-fish. Rather, it asserts that if they are mermaids then they are half-
fish. And this is diagrammed without including within it the diagram for “Some
mermaids are half-fish". Thus, to infer the truth of “Some mermaids are half-fish” from
the truth of “All mermaids are half-fish” is an invalid inference. In our discussion of the
rules method of testing validity, this was called the existential fallacy (Rule 5): “All S are
P” can be true without assuming there are any A's; but if "Some S are P” is assumed true,
then we are committed to believing that there exists at least one member of S, and that it
is also a member of P.
This is a very important feature of language, for it allows us to make statements such as
“All people caught cheating on the test are people who will be expelled from the
College.” without assuming that some one is caught cheating on the test. On the other
hand, many general statements are descriptive of plants, animals, people, and things that
do actually exist. We say that an A or E proposition has existential import if the subject
class of the proposition contains at least one actual individual. If this assumption is made,
then it is valid to infer a particular proposition from its subaltern universal, as was done
in the traditional square of opposition. Let us call a universal propositions that do not
assume the existence of members of their subject class a hypothetical universal; and let
us call a universal proposition that does assume the existence of members of its subject
class an existential universal. The difference between them maybe shown by means of
their Venn diagrams:
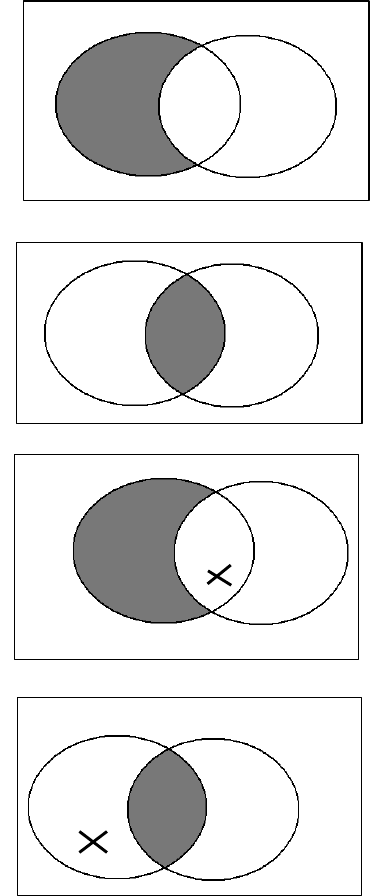
173
Hypothetical A:
Hypothetical E:
Existential A:
Existential E:
Figure 3.47
These diagrams clearly show that the truth of “Some S is P” can be inferred from “All S
and P” and the truth of “Some S are not P” can be inferred from “No S are P”. The
existential fallacy does not hold when we assume that the A and E propositions have
existential import.
S P
1 2 3
S P
1 2 3
S P
1 2 3
S P
1 2 3
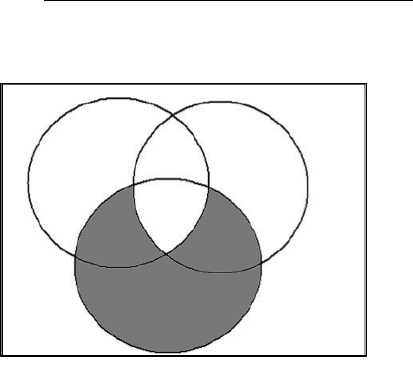
174
Let us now extend our use of existential A and E propositions in evaluating categorical
syllogisms by considering the syllogistic form AAI-3:
All M are P shade 4 & 7, x in 5 or 6
All M are S shade 6 & 7, x in 4 or 5
Some S are P x in 2 or 5
Figure 3.48
In diagramming the premises, we must do all of the shading first before we place the x so
that we do not mistakenly place it in an area that is empty (shaded). Had we not done this,
we could have mistakenly placed the x on the line that divides areas 5 and 6. But the
diagram of the minor premise shows that area 6 is empty. Therefore the correct place for
the x is in area 5. The x here tells us that the conclusion "Some S is P” is contained in the
premises. Hence, the argument form AAI-3 is valid.
1 2 3
S P
4 5 6
X
7
M S*P*M*
175
Let us next diagram the argument form EAO-3:
No M are P shade in 5 & 6, x in 4 or 7
All M are S shade in 6 & 7, x in 4 or 5
Some S are not P x in 4
Figure 3.49
Since there is an x in area 4, the diagram for the conclusion is contained in the diagram of
the combined premises. Therefore the argument form EAO-3 is valid.
Finally, let us diagram an invalid argument form: AAI-2
All P are M shade 2 & 3, x in 5 or 6
All S are M shade 1 &2
Some S are P x in 5
Figure 3.50
1 2 3
S P
4 5 6
7
M S*P*M*
1 2 3
S P
4 5 6
7
M S*P*M*

176
Note that while there might be an x in area 5, this is not necessarily so. Therefore the
diagram of the conclusion is not necessarily contained within the diagram of the
combined premises. Hence, the argument form, AAI-2 is invalid.
3.H.1 Exercises: Determine the validity of the following argument forms by means of
Venn diagrams that incorporate the existential assumption:
1. EIO-4 2. OAO-3 3. AEE-1 4. EIO-2
5. AOO-4 6. IAI-4 7. EAE-3 8. OAO-2
9. AOO-1 10. EIO-3 11. EIO-1 12. IAI-1
13. AOO-3 14. OAO-4 15. EAE-1
3.H.2. Exercises: Put each of the following syllogisms into standard form, give its
mood and figure, and test its validity by means of a Venn Diagram:
1. Some novelists are reformers, hence some Marxist are novelists, since all
Marxists are reformers.
2. Some animals are not four-legged creatures for no four-legged creatures are
birds and all birds are animals.
3. Some persons are not jobless individuals, but all welfare recipients are jobless
individuals; it follows that some persons are not welfare recipients.
4. Some football watchers are fanatics, so some people are fanatics, since all
football watchers are people.
5. All planes are fliers; therefore, no fliers are horses since no horses are planes.
177
6. No faint-hearted individuals were pioneers, for all faint-hearted individuals are
adventure-less persons and no pioneers were adventure-less persons.
7. No aliens are citizens and all aliens are foreign-born persons, consequently, no
citizens are foreign-born persons.
8. Some people are not Americans, for some people are not immigrants and some
immigrants are not Americans.
9. No economic system that favors the rich is a just one and all forms of
capitalism are economic systems that favor the rich, therefore, no just systems
are forms of capitalism.
10. No farmers are industrial workers because no farmers are factory workers and
all factory workers are industrial workers.
I. Enthymemes: How to Supply Unexpressed Premises and Conclusions
Now that we have studied the science and the art of determining valid categorical
syllogisms, one might justly ask how practical is the knowledge we have learned. In
everyday discourse, we do not hear people arguing by reciting syllogisms. How, then, can
we determine whether these arguments are valid or not? For example, someone might
say, “Okyere can become president of the United States because she was born in
America”. How can we test the validity of this type of argument?
An argument that is stated incompletely is called an enthymeme. The term is Greek and
literally taken, it means "in the mind". Thus, one of the premises of such an argument is
tacit, unexpressed, yet “in the mind” exerting an influence on the reasoning process. To
determine the validity of an enthymeme, we need to supply the unexpressed premise.
178
First, we look for the conclusion. From it we know the subject and predicate terms which
in turn tell us the major and minor premises. In the example above, the conclusion is
“Okyere can become president of the United States.” This means that the minor premise
is “Okyere is a native-born American.” The major premise is unexpressed, but we can
supply it. We know that it contains the predicate term, “can become president of the
United States,” and the middle term, “native-born American.'” Thus we can form the
major premise: All native-born Americans can become president of the United States.
The argument, completely stated, is thus:
All native-born Americans can become president of the United States.
Okyere is a native-born American.
Okyere can become president of the United States.
We can then restate the argument into Aristotelian propositions and proceed to test the
syllogism for validity.
The procedure for supplying the unexpressed premise is the same for enthymemes where
the minor premise is unexpressed: “Okyere can become president because all native-born
Americans can become president.”
If the conclusion is unexpressed, we must determine whether a valid conclusion can be
drawn from the premises given. Suppose we have the following premises:
All M is P.
Some M is S.
Now, what valid conclusion can we draw from the premises given? Is it valid to
conclude, “Some S is not P?” or “All S is P?” Knowledge of the rules will help us in
identifying a valid conclusion. We know that the conclusion always contains the terms S
and P, but from Rule 4 we know that the conclusion cannot be “Some S is not P” since a
negative conclusion requires a negative premise. And the conclusion “A1l S is P” cannot

179
be drawn either because it would violate Rule 2, which states that no term can be
distributed in the conclusion which is not distributed in the premise, which in this case is
the S term. Thus the valid conclusion would have to be “Some S is P.”
3.I.1. Exercises: Enthymemes
Supply the unexpressed premise of the following arguments:
1. All dentists are college graduates so all members of the American Dental
Association are college graduates.
2. I am a pessimist since I believe that there is more evil than good in the world.
3. Martin Luther King Jr. is a civil rights leader so he must be a supporter of freedom.
4. Premarital sex is immoral because any sex outside marriage is immoral.
5. No abortion is moral because abortion is the killing of an innocent person.
6. Any student who graduates from Farvard University is a well-educated person
because anyone who graduates from a prestigious university is a well-educated
person.
7. Mary knows math very well, so Mary must be a good math teacher.
8. All Wolves are Canines so all dogs are Canines.
9. Nuclear war kills massively and indiscriminately; therefore it is immoral.
10. No wealthy people are exploited; therefore no wealthy people support socialism.

180
11. According to Orthodox Jews, the West Bank belongs to Israel because Judea and
Samaria belong to Israel.
12. Romney is for the rich because he favors tax cuts.
3.I.2. Exercises: Drawing Conclusions from Premises
Draw a valid conclusion from the following premises:
1. All good orators are fluent speakers.
Some preachers are good orators.
__________________________________________
2. No vegetarian is a meat-eater.
Some vegetarians are men.
___________________________________________
3. All geniuses are intelligent people.
Some physicists are geniuses.
___________________________________________
4. No lady is a crude person.
Some women are crude persons.
___________________________________________
5. All victims of economic injustice are members of oppressed groups.
All poor people are victims of economic injustice.
_______________________________________________
181
6. No adult movies are films for children.
Some movies are adult movies.
________________________________________________
7. All supporters of democracy are lovers of freedom.
No dictators are lovers of freedom.
_________________________________________________
8. All killing of innocent persons is murder.
All abortions are killing of innocent persons.
_________________________________________________
9. No publishers of obscene and lewd magazines are decent and responsible citizens.
Some prosperous individuals are publishers of obscene and lewd magazines.
_____________________________________________________
10. No person who pays federal income tax should be denied voting representation in
Congress.
All residents of the District of Columbia pay federal income taxes.
_____________________________________________________
11. All great athletes are cool under pressure.
Tiger Woods is a great athlete.
_____________________________________________________
12. No Democrats are Republicans.
Abraham Lincoln was a Republican.
_____________________________________________________

182
13. All liberals are advocates of national health insurance.
Senator John Edwards is a liberal.
_____________________________________________________
14. No thoroughbred is a slow runner.
Seattle Slew is a thoroughbred.
_____________________________________________________
15. All Black people are humans.
All Congolese are Black people.
_____________________________________________________
3.I. 3. Exercises: For each of the following, supply the missing premise or conclusion that
produces the strongest argument.
1. All A are B and all B are C.
_________________________________________________________
2. All A are B because all B are C.
_________________________________________________________
3. All A are B and all C are B.
__________________________________________________________
4. All A are B because all C are B.
183
5. All A are B and all C are A.
_________________________________________________________
6. All A are B because all C are A.
___________________________________________________________
7. All A are B and some B are C.
___________________________________________________________
8. All A are B because some B are C.
___________________________________________________________
9. All A are B and some B are not C.
___________________________________________________________
10. All A are B because some B are not C.
___________________________________________________________
11. All A are B and some A are C.
___________________________________________________________
12. All A are B because some A are C.
____________________________________________________________
13. All A are B and some A are not C.
____________________________________________________________
14. All A are B because some A are not C.
_____________________________________________________________
184
15. All A are B and No B are C.
_____________________________________________________________
16. All A are B because No B are C.
_____________________________________________________________
17. All A are B and No A are C.
_____________________________________________________________
18. All A are B because No A are C.
_____________________________________________________________
19. All A are B and some C are not A.
_____________________________________________________________
20. All A are B because some C are not A.
______________________________________________________________
